上極限（読み）じょうきょくげん（その他表記）superior limit

改訂新版　世界大百科事典

上極限 (じょうきょくげん)
superior limit

実数列｛a_i｜i＝1，2，……｝があって，上に有界であるとき，各自然数nに対して，集合E_nをE_n＝｛a_i｜i≧n｝で定義すれば，これは上に有界であるので上限をもつ。E_nのそれぞれの上限をb_nとおくと，｛b_n｜n＝1，2，……｝は単調減少数列であるので，nを限りなく大きくしたとき，ある数αに収束する。このαを｛a_i｝の上極限といい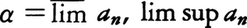，などで表す。また上極限αは，任意の正の数εに対して，α＋ε＜a_nとなるnは有限個，α－ε＜a_nとなるnは無限個存在するという性質をもつ数であるとして特徴づけることもできる。下極限inferior limitも大小関係を逆にして同様に定義され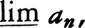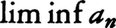，などと書く。例えば数列｛（－1）ⁿ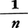＋｝の上極限は1，下極限は－1である。数列｛a_n｝に上極限α，下極限βが存在して一致すれば｛a_n｝はαに収束する。逆に｛a_n｝が極限値をもてば，｛a_n｝の上極限と下極限は一致する。上の数列｛（－1）ⁿ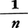＋｝は，上極限と下極限が異なり極限値をもたない。
執筆者：杉江 徹

出典　株式会社平凡社「改訂新版　世界大百科事典」