極限（読み）キョクゲン

デジタル大辞泉

きょく‐げん【極限】

１ 物事の限度ぎりぎりのところ。「体力の極限に達する」
２ 数列の項の番号を限りなく大きくするとき、または関数の変数の値をある値に近づけるか正・負の無限大にするときに、数列や関数値が限りなく近づく一定の値。極限値。
[類語]限度・限界・リミット・限り・最大限・手一杯・目一杯・頭打ち・際限・際きわ・上限・下限・北限・ぎりぎり・

出典　小学館

精選版 日本国語大辞典

きょく‐げん【極限】

1. 〘 名詞 〙
2. ① ( ━する ) 極めてせまい範囲に限定すること。
   1. [初出の実例]「人間の技倆は機械の働きの如く、世の進歩と逆比例に段々極限されて行かねばならぬ」(出典：女工哀史（1925）〈細井和喜蔵〉二)
3. ② 物事の限度ぎりぎりの所。
   1. [初出の実例]「恋とは夢だ。…『夢』とは全き放心だ。その正しい極限では一切が虚無となる」(出典：なよたけ（1946）〈加藤道夫〉第一幕)
4. ③ ＝きょくげんち（極限値）〔物理学術語和英仏独対訳字書（1888）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

極限
きょくげん

数列a₁, a₂,……, a_n,……において、添数のnが限りなく大きくなるとき、a_nの値がある値Aに限りなく近づくならば、a_nはAに収束するといい、Aをこの数列の極限値limit valueといって、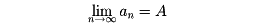

と書く。また、nを大きくするとき、a_nが限りなく大きくなるならば、a_nは正の無限大に発散するといい、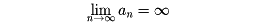

と書く。nを大きくするとき、a_nが負でその絶対値が限りなく大きくなるならば、a_nは負の無限大に発散するといい、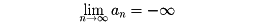

と書く。a_nがある極限値に収束する場合、あるいは正または負の無限大に発散するとき、極限があるといい、そうでないとき、極限がないという。数列の極限はこのように、数列においてnが限りなく大きくなるとき、a_nがどのようになるかを考えるための概念的な用語である。

［竹之内脩］

関数の極限

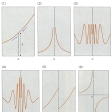
関数f(x)はx＝aの近くで定義されているとする（x＝aでは定義されていなくてもかまわない）。このときxが限りなくaに近づくときf(x)の値がどのようになっていくかが極限の問題である。

(1) f(x)はある定まった値bに限りなく近づく。このとき、f(x)はbに収束するといい、bを、xがaに近づいたときのf(x)の極限値といって、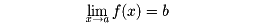

と書く（図の(1)）。

(2) f(x)はいかなる値をも超えて大きくなっていく。このときf(x)は正の無限大に発散するといって、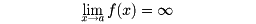

と書く（図の(2)）。f(x)が負の値をとって、その絶対値が限りなく大きくなるとき、f(x)は負の無限大に発散するという。以上が極限のある場合である。次に極限のない場合を考える。

(3) f(x)は有界（関数の値が、ある数を超えず、また、ある数より小さくならないとき、その関数を有界であるという）であるが極限のない場合（図の(3)）。

(4) f(x)は有界でなく極限のない場合（図の(4)）。

　なお極限のない場合、aの片側だけをみると極限のある場合もある（図の(5)・(6)）。左側から近づいたときの極限値があるとき、これを左側極限値といい、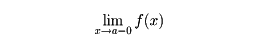

で表す。同様に、右側極限値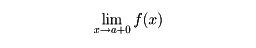

が定められる。

［竹之内脩］

[参照項目] | 収束 | 数列

極限（関数の極限）〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

極限 (きょくげん)
limit

数列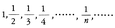を考えると，この数列の第n項は，nが限りなく大きくなるにつれて0に限りなく近づく。一般に一つの無限数列｛a_n｜n＝1，2，……｝の第n項a_nが，nを限りなく大きくするときある一定の数Aに限りなく近づくとき，この数列は収束するといい，Aをこの数列の極限値と呼ぶ。記号で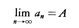，で表す。例えば数列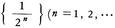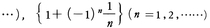は収束し，極限値はそれぞれ0，1である。収束しない数列を発散数列と呼ぶ。それらのうち，

（1）1，2，2²，2³，……，2ⁿのように，nが大きくなるに従って第n項a_nが限りなく大きくなるとき，この数列は正の無限大に発散するといい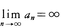，とかく。

（2）同様に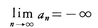の場合が定義される。

（3）その他の場合，その数列は振動すると呼ばれることがある。実数列が収束するために必要十分な条件は，それが基本列をなすことである。
執筆者：杉江 徹

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

極限【きょくげん】

→収束

出典　株式会社平凡社