二次形式（読み）にじけいしき（英語表記）quadratic form

改訂新版　世界大百科事典

二次形式 (にじけいしき)
quadratic form

x₁²＋4x₁x₂＋x₂²＝x₁²＋2x₁x₂＋2x₂x₁＋x₂²のように，いくつかの変数x₁，x₂，……，x_nの多項式で，すべての項が二次の項だけからなるものをx₁，x₂，……，x_nについての二次形式という。二次形式は対称行列（S＝^tSを満たす行列。ここで^tSはSの転置行列）を用いて，

と表される。上の例では，

である。QのことをSで決まる二次形式という。以下，（x₁，……，x_n）＝xと略記することにする。二次形式Qに対し，をQの極形式という。Qは，Bを用いてQ（x）＝B（x，x）と表される。Sの行列としての階数rをQの階数といい，Sが正則のときQは非退化であるという。これは，すべてのyに対してB（x，y）＝0となるxは0に限るということもできる。

　二次形式に適当な直交変換を行うことにより，

　α₁x₁′²＋……＋α_px_p′²－α_p+1x_p+1′²－

　　……－α_p+qx_p+q′²　（α₁＞0）　

という形にできる。このときp＋q＝r（rは階数）で，この（p，q）を二次形式の符号数といい，この形に変換することをQを主軸変換するという。

　二次形式において，すべてのxに対してQ（x）≧0で，Q（x）＝0となるのはx＝0に限るとき正値形式といい，Q（x）≦0でQ（x）＝0ならば，x＝0であるとき負値形式であるという。これ以外のときは不定値形式であるという。この三つの場合は，符号数を用いて（p，q）＝（n，0），（0，n），それ以外と区別できる。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

二次形式
にじけいしき

二変数の二次同次式ax²+bxy+cy²を二変数の二次形式という。形式は行列を用いて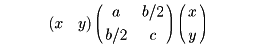

と表せる。同様に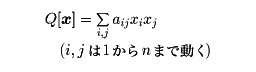

という二次の同次式をn変数の二次形式という。ただしa_ij=a_jiと決めておく。

　　A=(a_ij)
によってn次行列Aをつくれば、Aは対称行列である。

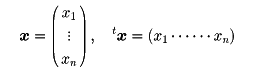
とすると、Q［x］は
　　Q［X］=^txAx
と表示できる。Uをn次行列として
　　x=Uy
という変換をすれば、二次形式は
　　^ty(^tUAU)y
と変換される。とくにAが実対称行列のとき、すなわちa_ijが実数のときには、正則行列Uを^tUAUが対角行列であるようにとれる。すなわち、適当な変数変換によって二次形式は
　　a₁x₁²+……+a_nx_n²
という標準形に変換できる。このa₁、……、a_nは並べ方を除けばもとの二次形式だけによって定まり、変数変換の仕方によらない。a₁、……、a_nがすべて正のとき正値形式、すべて負のとき負値形式という。

［足立恒雄］

[参照項目] | 行列

出典　小学館　日本大百科全書(ニッポニカ)