対称行列
たいしょうぎょうれつ
n次正方行列A=(aij)が
①aij=aji
(i,j=1,……,n)
を満たすとき、Aをn次対称行列という。①はAの主対角線に関して対称の位置にある行列成分が等しいことを意味するので、この名がつけられた。
条件①に対し、Aが
②aij=-aji
(i,j=1,……,n)
を満たすとき、Aをn次交代行列という。このとき、主対角線上の成分aiiは0になる。任意の正方行列Bに対し、tBをBの転置行列とすると、(B+tB)/2は対称行列、(B-tB)/2は交代行列で、
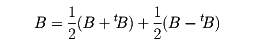
となる。実対称行列Aは適当に直交行列Pをとると、P-1APを対角行列にできる。この性質は二次形式に応用される。
[菅野恒雄]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
対称行列
たいしょうぎょうれつ
symmetric matrix
正方行列 A=(aij) において,主対角線に関して対称の位置にある2つの要素がそれぞれ等しいとき,すなわち aij=aji であるとき,この正方行列 A を対称行列という。これはまた A がその転置行列 tA に等しい行列,すなわち A=tA である場合といってもよい。たとえば,単位行列は対称行列である。また任意の行列 A とその転置行列 tA との和および積も対称行列になる。2次形式を行列で表現するときに用いられる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の対称行列の言及
【行列】より
…対角線より下(または上)の場所の成分が0の正方行列を上半(下半)三角行列,総称して単に三角行列という。tA=Aとなるとき,Aは対称行列であるという。実行列で,tA=A-1であるものを直交行列という。…
※「対称行列」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by