有界変動関数（読み）ゆうかいへんどうかんすう（英語表記）function of bounded variation

改訂新版　世界大百科事典

有界変動関数 (ゆうかいへんどうかんすう)
function of bounded variation

区間［a，b］で定義された関数f（x）に対して，区間の分割△：a＝x₀＜x₁＜……＜x_n＝bについて作った和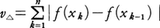，が，分割に無関係な定数を超えないとき，fは有界変動であるといい，あらゆる分割△を考えたときのv△の上限Vを，fの［a，b］における全変動という。有界変動関数は有界である。二つの有界変動関数f，gの一次結合および積は有界変動であり，さらに｜g（x）｜≧c＞0なるcがあればf（x）/g（x）も有界変動である。有界な単調関数は有界変動である。逆に任意の有界変動関数は二つの有界な単調増加関数の差として表される。有界変動関数の不連続点はたかだか可算無限個しかない。初めの分割△におけるf（x_k）－f（x_k-1）の中で正のもの，負のものの総和をそれぞれp△，－n△とし，p△，n△の上限をP，Nとすると，V＝P＋Nとなる。［a，b］内の1点xをとり，［a，x］において上のP，N，Vのように定義したものをP（x），N（x），V（x）とすると，

　V（x）＝P（x）＋N（x）

　f（x）－f（a）＝P（x）－N（x）

となる。P（x），N（x），V（x）をそれぞれfの正の変動，負の変動，全変動という。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」