核関数（読み）かくかんすう（英語表記）kernel function

改訂新版　世界大百科事典

核関数 (かくかんすう)
kernel function

フーリエ級数の基底をなす三角関数系をモデルとして起こった直交関数系の理論は，応用上重要な種々の線形微分方程式の固有関数系に裏づけられながら，古くから展開されてきている。直交関数系の理論をとくに複素関数論に応用したセゲーG.Szegöの研究に端を発し，ベルクマンS.Bergmanが多変数複素関数の研究において，はじめて核関数の概念を確立した。

　一般的にいうと，n次元複素領域D（n≧1，n＝1ならば複素平面の領域）における正則関数からなるヒルベルト空間Hで，点ζ∈Dごとに線形汎関数H∋f→f（ζ）∈Cが有界であるとき，f（ζ）＝（f，K_ζ）を満たすK_ζ∈Hが決まるが，このK_ζを核関数という。K_ζ（z）は完備な正規直交系｛φ_j｝によって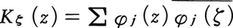，と表せる。

　HがDで2乗可積分な正則関数全体であり，内積が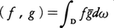ととられているときの核関数をベルクマン核関数という。ふつう独立変数をzとし，K_ζ（z）をK（z，ζ）と表す。

　Dが有界のときケーラー計量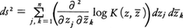，をベルクマン計量という。これは，n＝1でDが単連結のときは，ポアンカレ計量と本質的に一致する。平面領域Dにおいては，さらに別のHに別の内積を用いたセゲー核関数も導入されている。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」