精選版 日本国語大辞典 「内積」の意味・読み・例文・類語
ない‐せき【内積】
- 〘 名詞 〙 二つのベクトルの単位座標ベクトルに関する成分どうしの積の和。ベクトル
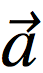 ,
,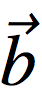 二つのなす角をθとするとき、|
二つのなす角をθとするとき、|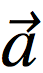 ||
||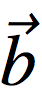 |cosθ の値をいう。
|cosθ の値をいう。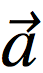 =(a1, a2),
=(a1, a2), 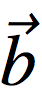 =(b1, b2) と成分表示するとき、内積は a1b1+a2b2 の値。スカラー積。
=(b1, b2) と成分表示するとき、内積は a1b1+a2b2 の値。スカラー積。
日本大百科全書(ニッポニカ) 「内積」の意味・わかりやすい解説
内積
ないせき
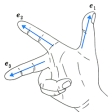
スカラー積ともいう。二つのベクトルの単位座標ベクトルに関する成分どうしの積の和をいう。たとえば三次元空間における内積とは、以下のようにして定まる実数値のことである。いま空間に単位座標ベクトルe1、e2、e3を定め、ベクトルの成分はこれに関して表すものとする()。二つのベクトル
a=(a1,a2,a3), b=(b1,b2,b3)
の内積(a,b)は、
(a,b)=a1b1+a2b2+a3b3
で定義される。aとbが0でないとき、それらのなす角をθとすれば、余弦定理によって
(a,b)=|a||b|cosθ
が成り立つ()。とくに、(a,a)=|a|2である。さらに、aとbが垂直であるとき(a,b)=0となり、a、bが単位ベクトルのとき(a,b)=cosθとなる。たとえば、いまe1、e2、e3を単位座標ベクトルとしているが、このことは、
(ei,ei)=1, (ei,ej)=0
(i,j=1,2,3 i≠j)
と書き表すことができる。このような性質をもつ座標ベクトルの組は、また内積に関する一つの正規直交系であるともいわれる。内積については次の法則が成り立つ。
(1)(a,a)≧0
もし(a,a)=0なら、a=0である
(2)(a,b)=(b,a)
(3)任意のスカラーkに対して
(ka,b)=k(b,a)
(4)(a+b,c)=(a,c)+(b,c)
これを一般化して、ベクトル空間の任意のベクトルa、bに対して実数(a,b)が定められていて、上の条件を満たすとき、(a,b)はaとbの内積という。
一方、単位座標ベクトルe1、e2、e3が右手系をなすとき、二つのベクトル
a=(a1,a2,a3), b=(b1,b2,b3)
に対して、これから定まる
(a2b3-a3b2,a3b1-a1b3,
a1b2-a2b1)
というベクトルをaとbの外積またはベクトル積といい、a×bと書く。a、bの一方が他方のスカラー倍になっているとき、a×b=0となる。そうでないとき、外積a×bは次のようにしてa、bから図形的に定まるベクトルになっている。において、a=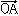 ,b=
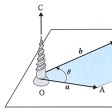
,b=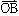 として、右ねじを平面OABのOのところに立てる(したがって、ねじはこの面に垂直となる)。このねじをaからbへ180度以内で回したとき、ねじの進む方向に点Cをとり、OCの長さがOA,OBを2辺とする平行四辺形の面積|a||b|sinθ(θ=∠AOB)に等しくなるようにする。このとき、a×b=
として、右ねじを平面OABのOのところに立てる(したがって、ねじはこの面に垂直となる)。このねじをaからbへ180度以内で回したとき、ねじの進む方向に点Cをとり、OCの長さがOA,OBを2辺とする平行四辺形の面積|a||b|sinθ(θ=∠AOB)に等しくなるようにする。このとき、a×b=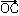 と表せる。外積については次の法則が成り立つ。
と表せる。外積については次の法則が成り立つ。
(a)a×b=-b×a
(b)任意のスカラーkに対して
(ka)×b=k(a×b)
(c)(a+b)×c=a×c+b×c
また、内積と外積について次のような代表的な関係式がある。
(イ)a×(b×c)=(a,c)b-(a,b)c
(ロ)(a,b×c)=(b,c×a)=(c,a×b)
[高木亮一]
ブリタニカ国際大百科事典 小項目事典 「内積」の意味・わかりやすい解説
内積
ないせき
inner product
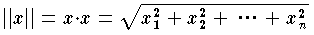 で定義する。内積の定義された空間を,一般に n次元ユークリッド・ベクトル空間または単に n次元ユークリッド空間と呼んでいる。相対論などでは,定符号でない内積を考えるが,この場合には性質(d)が成立しない。また,空間が複素空間であれば成分は複素数となり,yi の共役複素数を ȳi とするとき,内積を x・y=x1ȳ1+x2ȳ2+…xnȳn で定義する。この共役複素数
で定義する。内積の定義された空間を,一般に n次元ユークリッド・ベクトル空間または単に n次元ユークリッド空間と呼んでいる。相対論などでは,定符号でない内積を考えるが,この場合には性質(d)が成立しない。また,空間が複素空間であれば成分は複素数となり,yi の共役複素数を ȳi とするとき,内積を x・y=x1ȳ1+x2ȳ2+…xnȳn で定義する。この共役複素数 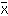 1y1+
1y1+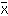 2y2+…,
2y2+…,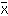 nyn と定義することもある。この場合,性質(a)が x・y=y・x(エルミート性)に変わること以外は実数空間と同様の議論が成り立つ。
nyn と定義することもある。この場合,性質(a)が x・y=y・x(エルミート性)に変わること以外は実数空間と同様の議論が成り立つ。(2) 関数空間の内積 二つの複素関数 f(x),g(x)に対して区間[a,b]上での内積を次式で定義する。
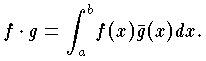 このような場合を含めて,内積をもった空間を内積空間または前ヒルベルト空間といい,それから決まるノルムの収束について完備なときヒルベルト空間という。関数系 fi(x)(i=1,2,3,…)が内積
このような場合を含めて,内積をもった空間を内積空間または前ヒルベルト空間といい,それから決まるノルムの収束について完備なときヒルベルト空間という。関数系 fi(x)(i=1,2,3,…)が内積 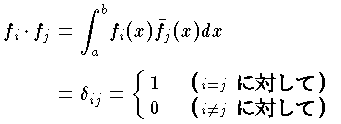 をもつとき,正規直交関数系であるという。
をもつとき,正規直交関数系であるという。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「内積」の意味・わかりやすい解説
内積【ないせき】
→関連項目ヒルベルト空間|ベクトル
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の内積の言及
【スカラー積】より
…平面のベクトルa,bを成分で書いて,a=(a1,a2),b=(b1,b2)とする。このとき,(a,b)=a1b1+a2b2をaとbのスカラー積,または内積という。このスカラー積については,(1)(a+b,c)=(a,c)+(b,c),(2)(b,a)=(a,b),(3)スカラーαについて,(αa,b)=α(a,b),(4)a≠0ならば(a,a)>0が成立する。…
【ベクトル】より
…一次独立なベクトルa,b,cが与えられれば,かってなベクトルはαa+βb+γcと書ける。 二つのベクトル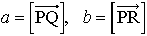 の内積を|a||b|cos(∠QPR)と定め,(a,b)またはa・bで表す。(a,b)=(b,a),(a+b,c)=(a,c)+(b,c),実数αについて,(αa,b)=α(a,b)が成立する。…
の内積を|a||b|cos(∠QPR)と定め,(a,b)またはa・bで表す。(a,b)=(b,a),(a+b,c)=(a,c)+(b,c),実数αについて,(αa,b)=α(a,b)が成立する。…
【ベクトル空間】より
… 一般に集合Vにスカラー倍,和が定まって,上記(1)~(8)を満たすとき,Vはベクトル空間であるといい,Vの元をベクトルと呼ぶ。ベクトル空間Vの任意の二元a,bについて,実数(a,b)が定まり,(a+b,c)=(a,c)+(b,c),(a,b)=(b,a),(αa,b)=α(a,b),さらに(a,a)=0ならば,a=0であるという性質をもつとき,(a,b)をaとbの内積という。この内積に関するベクトルaの長さ|a|は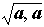 と定める。…
と定める。…
【ユニタリ変換】より
…U*U=UU*=1(単位行列)なる正方行列Uをユニタリ行列といい,ユニタリ行列で表されるCnの一次変換φをユニタリ変換という。Cnの二つのベクトル,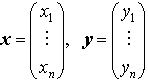 に対して,
に対して,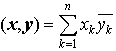 をxとyとの内積といい,また,
をxとyとの内積といい,また,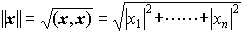 をxの長さという。ユニタリ変換φは内積および長さを不変にする。…
をxの長さという。ユニタリ変換φは内積および長さを不変にする。…
※「内積」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

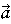 ,
, 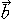 があって、二つのなす角をθとするとき、|
があって、二つのなす角をθとするとき、|