準同形 じゅんどうけいhomomorphic

ブリタニカ国際大百科事典 小項目事典の解説

準同形
じゅんどうけい
homomorphic

たとえば群から群へというように，同種の2つの代数系 X，Y の間に対応 f：X→Y が，x∈X に対し f(x)＝y∈Y を対応させるような対応として存在し，しかもこの対応 f が，その演算を保存するとき，f は X から Y への準同形写像であるといい，この準同形写像が X から Y の上への写像，すなわち全射であるとき，Y は X に準同形であるという。 X，Y がともに群のとき，その演算・が保存されるとは，f(x・y)＝f(x)・f(y) が成り立つことを意味する。 X，Y がともに環あるいは体のときは，演算＋および・に関して
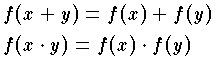が成り立つことであり，X ，Y がともに束ならば，演算 ∪ ，∩ に対して，

f(x∪y)＝f(x)∪f(y)，f(x∩y)＝f(x)∩f(y)

が成り立つことである。 X，Y がともにベクトル空間の場合は，その演算であるスカラー倍と加法に対して，

f(ax)＝af(x)，f(x＋y)＝f(x)＋f(y)

が成り立つことである。特に f が X から X への準同形である場合，すなわち1つの代数系の自分自身への写像であるときは，この f を自己準同形写像という。

出典｜ブリタニカ国際大百科事典 小項目事典