準同形写像（読み）じゅんどうけいしゃぞう

日本大百科全書(ニッポニカ)

準同形写像
じゅんどうけいしゃぞう

群Gから群G′の上への写像fが、Gの任意の元a、bに対して
　　f(ab)＝f(a)f(b)
という性質をもつとき、fを群Gから群G′の上への準同形写像という。たとえば、正の数の全体の乗法による群をG、実数全体の加法による群をG′とするとき、
　　f(x)＝logx
は、GからG′の上への準同形写像である。また、実数上のn次の正則行列（逆行列の存在する行列）の全体の乗法による群（一般線形群）をGL(n, R)とし、ゼロを除く実数全体の乗法による群をR^xとするとき、正則行列Aに対して
　　f(A)＝|A|　（Aの行列式）
は準同形写像である。

　群Gから群G′の上への準同形写像fが、とくに1対1の写像であるとき、fはGからG′の上への同形写像とよばれる。前に述べた初めの例の、f(x)＝logxは同形写像であるが、後の例のf(A)＝|A|は同形写像ではない。

［寺田文行］

準同形定理

同形写像についての基本定理は準同形定理である。まずfが群Gから群G′の上への準同形写像のとき、fによって群G′の単位元に写像されるGの元の全体をNとすると、Nは群Gの正規部分群である。Nは準同形写像fの核とよばれ、このNによって群Gの商群G/Nをつくる。G/Nの元はaNと表され、群G/Nから群G′への写像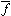を次のように定義する。

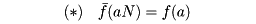
すると次の定理が成り立つ。「群Gから群G′への上への準同形な写像fがあるときfの核をNとすると（＊）で定義される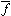は商群G/NからG′の上への同形写像である」。これを準同形定理という。たとえば、前述の実数上の一般線形群GL(n, R)から、実数の乗法群R^xへの準同形写像f(A)＝|A|においては、核Nは|A|＝1となる行列Aの全体である。このNを特殊線形群といい、SL(n, R)で表される。前述の準同形定理によれば、行列の行列式を考えることによって同形写像
　　GL(n, R)/SL(n, R)→R^x
が得られることになる。

［寺田文行］

出典　小学館　日本大百科全書(ニッポニカ)