複素積分（読み）ふくそせきぶん（その他表記）complex integral

ブリタニカ国際大百科事典 小項目事典

複素積分
ふくそせきぶん
complex integral

複素平面上に，なめらかな曲線 C：z＝z(t)(a≦t≦b) と，曲線 C に沿って連続な複素関数 f(z) が与えられているとする。このとき，区間 [a，b] を a＝t₀＜t₁＜t₂＜…＜t_n-1＜t_n＝b で細分し，区間 [t_k-1，t_k] の中に任意に点 τ_k をとり，
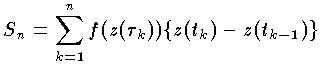をつくる。このとき，｜z(t_k)－z(t_k-1)｜ のうちの最大のものが0に近づくように n→∞ とすれば，上の S_n は，分点 t_k ，区間 [t_k-1，t_k] 中の τ_k のとり方いかんにかかわらず，1つの極限値に近づく。これを f(z) の C に沿っての複素積分と呼び，
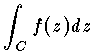で表わす。

出典　ブリタニカ国際大百科事典 小項目事典