翻訳|curve
精選版 日本国語大辞典 「曲線」の意味・読み・例文・類語
きょく‐せん【曲線】
- 〘 名詞 〙
- ① 角ばらないで、連続的に曲がった線。カーブ。
- [初出の実例]「直線 曲線 波線」(出典:小学教授書(1873)〈文部省〉)
- ② 区間から平面ないしは空間への連続写像。または、それによる区間の像。
改訂新版 世界大百科事典 「曲線」の意味・わかりやすい解説
曲線 (きょくせん)
curve
通俗には直線でない線を曲線と呼び,数学の古典であるユークリッドの《ストイケイア》もこの立場をとっている。しかしながら,現今の数学では曲線は線の同義語で,直線をもその中に含める。ユークリッドは〈線とは幅のない長さで,その端は点である〉と述べ,線すなわち曲線の一応の説明をしている。しかしこれは完全な定義とはいえない。ユークリッド以後は19世紀後半まで,曲線は自明な概念として定義も与えられず使われてきたが,今日では曲線を解析的表示によって定義する。
平面曲線
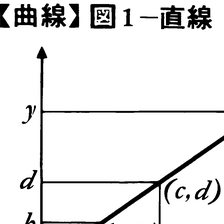
まず,平面曲線,すなわち1平面上に乗っている曲線について述べよう。これは点が平面上を動いたときにできる図形と考えられる。したがって,平面上に直交座標を導入し,時刻tにおける点の位置を(x,y)とすれば,x,yはtの関数f(t),g(t)で表される。さらに,ある区間内のすべてのtに対し(f(t),g(t))を座標とする点を考えれば,これらの全体がもとの曲線となる。このようなわけで,平面曲線とは,f,gをある区間で定義された関数として,その区間に属するすべてのtに対し,点(f(t),g(t))を考えたときにできる図形といえる。この曲線をx=f(t),y=g(t)で表し,これを媒介変数tによる媒介変数表示という。例えば,2点(a,b),(c,d)を通る直線は全区間(-∞,∞)に属するtを媒介変数として,x=a+(c-a)t,y=b+(d-b) tと表され(図1),(a,b)を中心とする半径rの円周は,閉区間[0,2π]に属するtを媒介変数として,x=a+r cos t,y=b+r sin tと表される(図2)。関数y=f(x)のグラフはx=t,y=f(t)と媒介変数表示される。f,gが連続関数ならば,x=f(t),y=g(t)で表される曲線を連続曲線という。f,gの定義域が閉区間[a,b]のときの連続曲線を弧または道という。このとき,(f(a),g(a))を始点といい,(f(b),g(b))を終点という。両者を合わせて端点という。端点の一致する弧を閉曲線またはループloopという。t≠t′で(f(t),g(t)),(f(t′),g(t′))が同じ点を表すとき,この点を重複点という。重複点をもたない弧を単純弧といい,端点以外には重複点をもたない弧を単一閉曲線simple closed curveまたはジョルダン曲線Jordan curveという。単純弧は線分に,単一閉曲線は円周に同位相である。単一閉曲線は平面を内部と外部の二つの領域に分ける。単一閉曲線とその内部の点からなる集合の任意の2点がつねにその集合内にある線分で結べるとき,もとの単一閉曲線を卵形線ovalまたは凸閉曲線という。連続曲線の中には,正方形の内部をうめつくす弧(ペアノ曲線)や一つも接線の引けない単一閉曲線のようなものが存在する。このような病的症状を呈する曲線や,弧が点に退化するような曲線をさけ,さらに曲線の滑らかさを保証するため,通常,曲線というときは,ほとんどすべてのtに対し,f(t),g(t)は何回でも微分可能で,微分f′(t),g′(t)は同時には0にならないと仮定する。f,gの定義域内にあるa,bに対し,積分,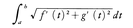 を点(f(a),g(a))から点(f(b),g(b))までの弧長という。曲線上に1定点をとるとき,曲線上の点は定点からその点までの弧長で定まり,したがって曲線は弧長を媒介変数として表される。この媒介変数表示は有用でしばしば用いられる。先にあげた円周の媒介変数表示はr=1のときにはこの表示になっている。
を点(f(a),g(a))から点(f(b),g(b))までの弧長という。曲線上に1定点をとるとき,曲線上の点は定点からその点までの弧長で定まり,したがって曲線は弧長を媒介変数として表される。この媒介変数表示は有用でしばしば用いられる。先にあげた円周の媒介変数表示はr=1のときにはこの表示になっている。
曲線Cの媒介変数表示x=f(t),y=g(t)よりtを消去すれば,F(x,y)=0という形の方程式が得られる。この方程式は曲線C上の点のx座標とy座標の間に成り立つ関係式を表し,また曲線Cを表している。この方程式F(x,y)=0を曲線Cの方程式と呼ぶ。例えば,2点(a,b),(c,d)を通る直線の方程式は(d-b)(x-a)-(c-a)(y-b)=0で,(a,b)を中心とする半径rの円周の方程式は(x-a)2+(y-b)2-r2=0である。F(x,y)=0がyについて解けてy=f(x)の形となるときは,F(x,y)=0の表す曲線は関数y=f(x)のグラフである。曲線は極座標を用いてG(r,θ)=0のようにも表すことができる。F(x,y)がx,yについての多項式のとき,F(x,y)=0で表される曲線を代数曲線といい,多項式の次数がnのとき,これをn次曲線という。一次曲線は直線で,二次曲線は円錐曲線(楕円,双曲線,放物線および交わる2直線)である。代数曲線でない曲線を超越曲線という。たとえば,y=exやy=sin xのグラフとして現れる指数曲線や正弦曲線は超越曲線である。
空間曲線
空間内の曲線を空間曲線という。空間の点を直交座標を用いて(x,y,z)で表すとき,平面曲線のときと同様に,空間曲線はf,g,hをある区間で定義された関数として,x=f(t),y=g(t),z=h(t)のように媒介変数表示される。例えば,水平面に垂直に立てた半径aの直円柱面上にあって一定のこう配tをもつ図3のようなつるまき線の方程式は,図に示したような座標軸をとれば,x=a cos t,y=a sin t,z=bt(b=a tan t)と媒介変数表示される。空間曲線はまたその媒介変数表示から媒介変数を消去して得られるF(x,y,z)=0,G(x,y,z)=0のような連立方程式でも表される。これは空間曲線は一般に二つの曲面の交わりであることに相当する。空間曲線についても,閉曲線,長さ,代数曲線などの概念が平面曲線の場合と同様に定義される。
縮閉線,伸開線
平面曲線C上の1点Pに対し,Pとこれに近いC上の2点Q,Rを通る円を考える。この円のQ,RをCに沿ってPに近づけたときの極限の円をPにおけるCの曲率円という。Cの各点における曲率円の中心の描く曲線をΓとするとき,ΓをCの縮閉線またはエボリュートevoluteといい,CをΓの伸開線またはインボリュートinvoluteという。伸開線CはΓにまきつけた糸をピンと張りながらほぐしていったときの糸の端点が描く曲線である(図4)。
いろいろな平面曲線
次に歴史的によく知られた特殊な平面曲線を列挙する。
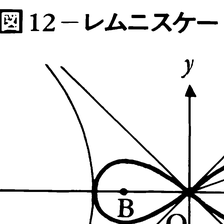
(1)方程式y2(a-x)=x3(aは正の定数)で表される三次曲線を疾走線またはシッソイドcissoidという(図5)。原点Oと点A(a,0)を結ぶ線分を直径とする円を考え,この円周上の動点Qに対し,直線OQと直線x=aとの交点をRとして,線分OQ上に点PをOPとQRの長さが等しくなるようにとれば,Pはこの曲線を描く。(2)方程式(x-a)2(x2+y2)=b2x2(a,bは正の定数)で表される四次曲線をコンコイドconchoidまたは螺獅(らし)線という(図6)。直線x=a上の動点Qに対し,直線OQ上に長さbの線分QPをQの両側にとれば,Pはこの曲線を描く。(3)方程式(x2+y2-ax)2=b2(x2+y2)(a,bは正の定数)で表される四次曲線をリマソンlimaçonまたは蝸牛(かぎゆう)線という(図7)。原点OとA(a,0)を結ぶ線分を直径とする円周上に動点Qをとり,直線OQ上に長さbの線分QPをQの両側にとるとき,Pはこの曲線を描く。a=bの場合のリマソンはふつうカージオイドcardioidまたは心臓形と呼ばれる(図8)。一般に,1定点Oから定曲線Cの各接線に下ろした垂線の足の描く曲線をCのOに関する垂足曲線pedal curveという。Aを中心とする半径bの円を考えるとき,リマソンはこの円の原点Oに関する垂足曲線である(図9)。以上の(1)(2)(3)は立方倍積問題や角の三等分問題を解くのに利用された曲線である。(4)方程式x3+y3=3axy(aは正の定数)で表される三次曲線をデカルトの葉線folium of Descartesという(図10)。楕円x2-xy+y2-ax-ay=0上の動点Qに対し,直線OQと直線x+y+a=0との交点をRとして,線分OQ,ORのうちの長いほうの上に点PをOPの長さがOQとORの長さの差に等しくなるようにとれば,Pはこの曲線を描く。(5)方程式(x2+y2)2-2a2(x2-y2)=b4-a4(a,bは正の定数)が表す四次曲線をカッシーニ曲線Cassini’s curveという(図11)。これは2点A(a,0),B(-a,0)からの距離の積がb2に等しいような点Pの描く曲線である。b=aの場合のカッシーニ曲線,すなわち(x2+y2)2=2a2(x2-y2)の表す曲線をふつうレムニスケートlemniscateまたは連珠形という。これは直角双曲線x2-y2=2a2の原点Oに関する垂足曲線である(図12)。(6)定曲線Cに接しながら,その上を他の曲線Γがすべらないでころがるとき,Γに対し固定された点Pの描く曲線をルーレットrouletteまたは輪転曲線といい,Cを底線,Γを転曲線,Pを極という。底線が直線で,転曲線が円周であるルーレットは,極が転曲線上にあるときにはサイクロイドcycloidまたは擺(はい)線,そうでないときにはトロコイドtrochoidと呼ばれる(図13,14)。転曲線である円の半径をa,その中心から極までの距離をbとすれば,トロコイドは回転角tを媒介変数として,x=at-b sin t,y=a-b cos tと表される。ここでa=bとすればサイクロイドを表す式となる。底線,転曲線がともに円で,これら2円が外接(内接)する場合のルーレットは,極が転曲線上にあるときには,外サイクロイド(内サイクロイド)またはエピサイクロイドepicycloid(ハイポサイクロイドhypocycloid)と呼ばれ,そうでないときには外トロコイド(内トロコイド)またはエピトロコイドepitrochoid(ハイポトロコイドhypotrochoid)と呼ばれる(図15,16)。底線の円の半径をa,転曲線の円の半径をb,転曲線の円の中心と極の距離をcとするとき,転曲線の回転角tを媒介変数として,外トロコイド,内トロコイドはx=(a±b)cos t∓c cos((a±b)/b)t,y=(a±b)sin t-c sin((a±b)/b)t(複号同順)で表される。ここでb=cとすれば外サイクロイド,内サイクロイドを表す式となる。a=bの場合の外サイクロイドはカージオイドである(図17)。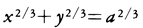 (aは正の定数)で表される曲線をアステロイドasteroidまたは星芒(せいぼう)形という。これはa=4bの時の内サイクロイドである(図18)。(7)双曲線余弦関数
(aは正の定数)で表される曲線をアステロイドasteroidまたは星芒(せいぼう)形という。これはa=4bの時の内サイクロイドである(図18)。(7)双曲線余弦関数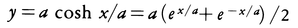 のグラフをカテナリーcatenaryあるいは懸垂線という(図19)。これはx軸を底線,放物線y=x2/(4a)を転曲線,この放物線の焦点A(0,a)を極とするルーレットである。この曲線のAからでる伸開線の方程式は
のグラフをカテナリーcatenaryあるいは懸垂線という(図19)。これはx軸を底線,放物線y=x2/(4a)を転曲線,この放物線の焦点A(0,a)を極とするルーレットである。この曲線のAからでる伸開線の方程式は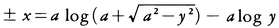
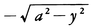 である。この曲線をトラクトリックスtractrixという。この曲線上の点Pにおける接線とx軸との交点をQとすれば,PQの長さはつねにaである(図20)。(8)極座標を用いてr=f(θ)(fは単調)で表されるような曲線を一般に螺線,スパイラルspiral,渦巻線などと呼ぶ。とくに,r=aθ,r=aebθ,r=a/θ(a,bは定数)で表される曲線をそれぞれアルキメデスの螺線Archimedes'spiral,対数螺線logarithmic spiral(等角螺線equiangular spiral),双曲螺線hyperbolic spiralという(図21)。
である。この曲線をトラクトリックスtractrixという。この曲線上の点Pにおける接線とx軸との交点をQとすれば,PQの長さはつねにaである(図20)。(8)極座標を用いてr=f(θ)(fは単調)で表されるような曲線を一般に螺線,スパイラルspiral,渦巻線などと呼ぶ。とくに,r=aθ,r=aebθ,r=a/θ(a,bは定数)で表される曲線をそれぞれアルキメデスの螺線Archimedes'spiral,対数螺線logarithmic spiral(等角螺線equiangular spiral),双曲螺線hyperbolic spiralという(図21)。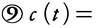
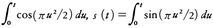 とおくとき,tを媒介変数として,
とおくとき,tを媒介変数として,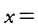
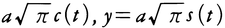 で表される曲線をコルニュの螺線Cornu's spiralまたはクロソイドclothoidという(図22)。
で表される曲線をコルニュの螺線Cornu's spiralまたはクロソイドclothoidという(図22)。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「曲線」の意味・わかりやすい解説
曲線
きょくせん
curve
平面、あるいは空間内で、その点の座標が一つの実変数tの連続関数となっているものを曲線、または連続曲線という。平面内の曲線を平面曲線といい、方程式
x=f(t), y=g(t)
で表される。空間内の曲線を空間曲線といい、
x=f(t), y=g(t), z=h(t)
で表される。
曲線はまた、
F(x, y)=0
あるいは
F(x, y, z)=0, G(x, y, z)=0
の形で与えられることもある。たとえば円は、
x=r cos t, y=r sin t
あるいは
x2+y2=r2
の形で与えられる。
平面曲線はまた、y=u(x)あるいは極座標によってr=v(θ)で与えられることもある。以下では、おもに平面曲線を考える。
「アステロイド」「カージオイド」「クロソイド」「コンコイド」「サイクロイド」「疾走線(しっそうせん)」「トラクトリックス」「螺線(らせん)」「リマソン」などの個々の曲線については、各項目を参照されたい。
[竹之内脩]
滑らかな曲線
平面曲線x=f(t), y=g(t)において、f(t), g(t)が導関数を有し、かつそれらが連続であるとき、この曲線を滑らかな曲線という。そして、f′(t), g′(t)を成分とするベクトル(f′(t), g′(t))を接ベクトルという。滑らかな曲線とは、接ベクトルが連続的に変わっていく曲線、という意味である。接ベクトルは、曲線上の近い2点
P(t)=(f(t), g(t))
P(t+Δt)=(f(t+Δt), g(t+Δt))
を結ぶベクトルをΔtで割って極限をとったものである。
[竹之内脩]
曲線の長さ
2点A、Bを結ぶ曲線があるとき、この曲線上でA、Bの間に順に数多くの点
P1, P2,……, Pn-1 (A=P0, B=Pn)
をとり、これらの点を次々と線分で結んで折れ線をつくる。この折れ線の長さ(各線分の長さの和)が、点のとり方をこの曲線上密になるようにしていったとき、ある極限値に収束するならば、この曲線は長さがあるといい、この極限値を曲線の長さという。
滑らかな曲線は長さを有し、その長さは次のようになる。
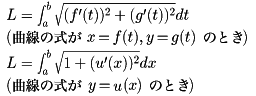
たとえば、円の場合は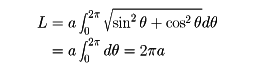
となり、周知の値を得る。また、放物線y=x2のx=aからx=b(a<b)までの長さは、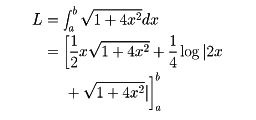
曲線の式がF(x, y)=0の形で与えられているとき、もしもある点で∂F/∂x=0,∂F/∂y=0が成り立っていると、この点の近くでは一般にF(x, y)=0をx=f(t), y=g(t)の形に表すことができない。これを、この曲線の特異点という。
曲線の式が与えられたとき、この曲線の概形を描くことを、曲線の追跡という。このためには、曲線の存在する範囲や、特異点、漸近線(ぜんきんせん)などを調べるとよい。
円のように両端がつながっている曲線を閉曲線という。レムニスケートのように自分自身と交わりをもつ閉曲線もある。自分自身と交わりをもたない閉曲線を単純閉曲線、あるいはジョルダン閉曲線という。ジョルダンは次のことを示した(1893)。「平面内の単純閉曲線は、平面を内部と外部の二つの部分に分け、内部の点と外部の点は、この曲線と交わることなしには結べない」。これをジョルダンの曲線定理という。内容は常識的であるが、数学的に証明しようとするとむずかしい定理である。
[竹之内脩]
『栗田稔著『いろいろな曲線』(1966・共立出版)』
百科事典マイペディア 「曲線」の意味・わかりやすい解説
曲線【きょくせん】
→関連項目弧|線
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「曲線」の意味・わかりやすい解説
曲線
きょくせん
curve
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...