随伴微分作用素（読み）ずいはんびぶんさようそ（その他表記）adjoint differential operator

改訂新版　世界大百科事典

随伴微分作用素 (ずいはんびぶんさようそ)
adjoint differential operator

区間（a，b）においてr回連続微分可能な関数の全体をC^rと書く。関数u∈C^rに作用する微分作用素，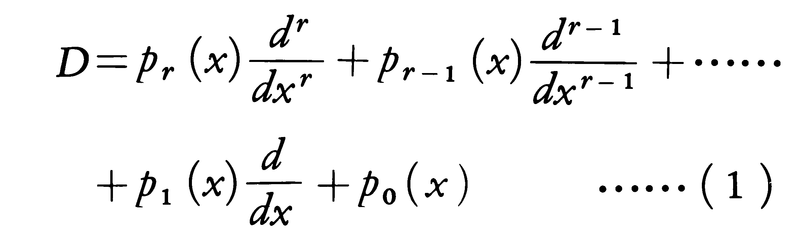

においてp_k∈C^k（k＝0，1，……，r）とする。これに対して，v∈C^rに作用する微分作用素，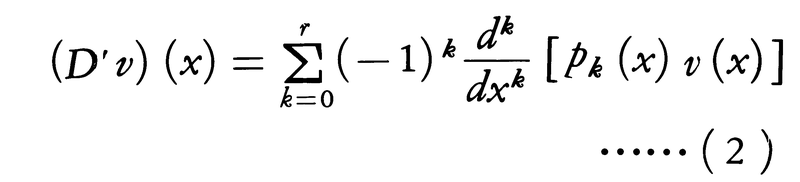

を考えると，u，v∈C^rであってa，bの近くではu，vの少なくとも一方が恒等的に0となるならば，部分積分により，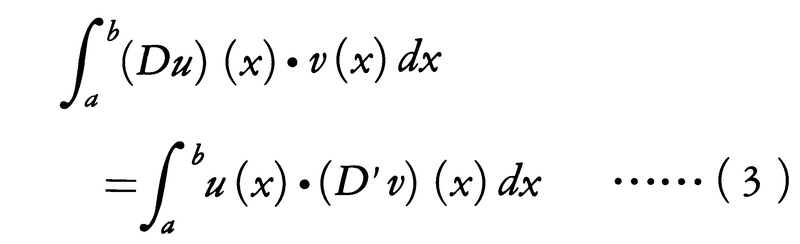

が成立する。このような関係にある微分作用素D′をDの随伴微分作用素という。このとき（D′）′＝Dであることも部分積分によってわかる。多変数の偏微分作用素についても同様である。n次元の領域Ωにおいてr回連続微分可能な関数の全体をC^rとし，u∈C²に対して，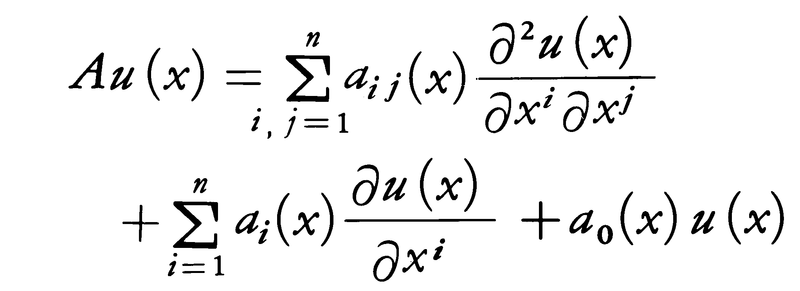

なる偏微分作用素Aを考える。ただしa_ij∈C²，a_i∈C¹とし，a₀は連続関数とする。このとき，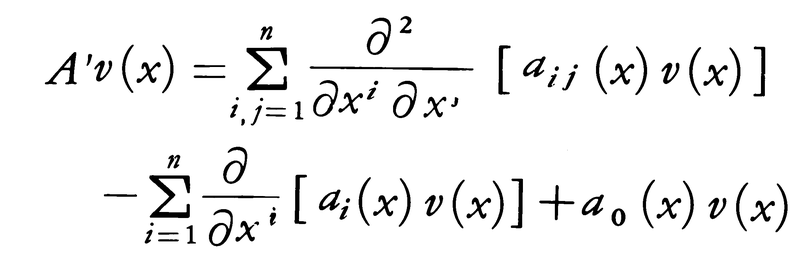

とすると，u，v∈C²であってΩの境界の近くではu，vの少なくとも一方が恒等的に0ならば，部分積分によって（3）と同様な式，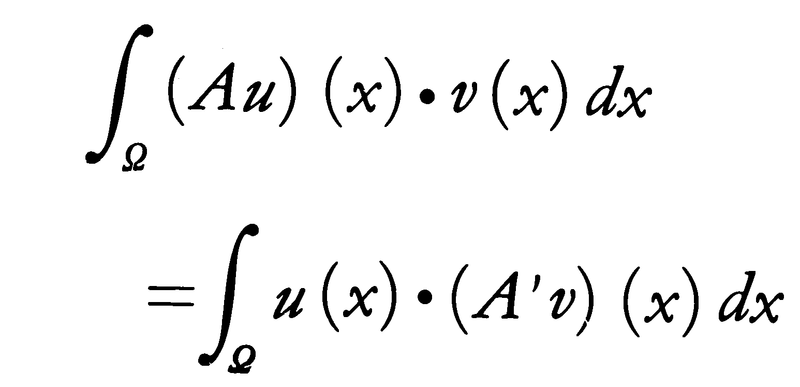

が成立する。すなわちA′はAの随伴微分作用素である。この場合も1変数の場合と同様に（A′）′＝Aなることが部分積分でわかる。とくに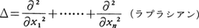，についてはΔ′＝Δである。
→微分作用素
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」