微分作用素（読み）ビブンサヨウソ（その他表記）differential operator

デジタル大辞泉

びぶん‐さようそ【微分作用素】

微分の演算で関数として定義された作用素。一階微分であればd/dx、n階微分であればdⁿ/dxⁿなどと書かれる。

出典　小学館

改訂新版　世界大百科事典

微分作用素 (びぶんさようそ)
differential operator

区間（a，b）で連続微分可能な関数f（x）にその導関数f′（x）を対応させることを考える。また，区間（a，b）で連続な関数p（x），q（x）が与えられたとき，この区間で2回連続微分可能な関数f（x）にf″（x）＋p（x）f′（x）＋q（x）f（x）を対応させることを考える。これらの例のように，関数から関数への対応f→Dfがあって，関数Dfの点xにおける値（Df）（x）がfおよびその有限個の導関数のxにおける値によって定まるとき，Dを微分作用素という。上の二つの例は，それぞれ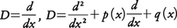，と表される。1変数の微分作用素は一般に，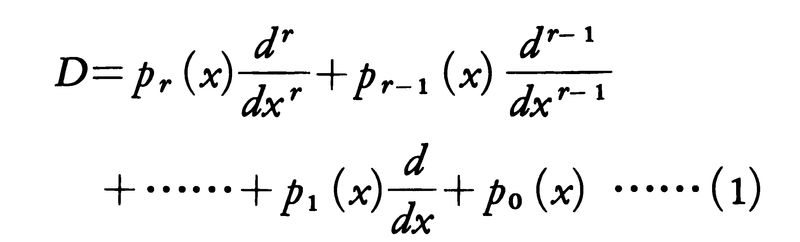

の形に書かれる。ここでp_k（x）（k＝0，1，……，r）は区間（a，b）において与えられた連続関数である。多変数の関数に対する微分作用素も同様に考えられる。例えばn次元空間の中の領域Ωで連続な関数a_ij（x），a_i（x）（i，j＝1，……，n）およびa₀（x）が与えられたとする。このとき，Ωで2回連続微分可能な関数u（x）に対し，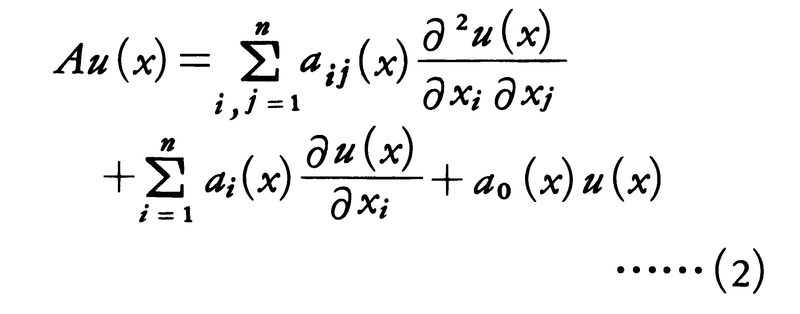

なるAは微分作用素であって，この場合は偏微分作用素とも呼ばれる。とくに偏微分作用素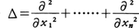は重要で，ラプラシアンLaplacian，またはラプラス作用素と呼ばれる。関数解析学では，考察する関数空間を定めて，微分作用素を関数空間から関数空間への写像として取り扱う。例えばn次元の有界領域Ωの閉包Ωにおいて連続なr階偏導関数をもつ関数の全体をC^rとする（C⁰はΩ上の連続関数の全体とする）とき，（2）においてa_ij，a_i，a₀がΩで連続ならば，（2）の微分作用素Aは関数空間C²からC⁰への作用素である。またΩが一次元の区間（a，b）のとき，（1）においてp_k（x）（k＝0，1，……，r）が閉区間［a，b］で連続ならば，（1）の微分作用素DはC^rからC⁰への作用素である。
→関数解析学
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」