高木‐トーパンの式（英語表記）Takagi-Taupin equation

法則の辞典

高木‐トーパンの式【Takagi-Taupin equation】

別名を「高木の方程式」という．1962年に（当時東京大学教授）高木佐知夫の導いた，歪みを含む不完全結晶にも適用可能な動力学的回折理論の基礎方程式である．

結晶内にX線や電子線が入射したとき，多くの回折波が生じるために，それらを含めた波の波動関数は振幅変調を受けた多数の波の重畳したものとして

ψ（r）＝∑ψh（r）exp（2πik_h・r）

のようになる．k_h は波動ベクトルであり，ψh（r） は振幅と位相を表す複素振幅である（ここまではトーパン（D. Taupin）がこれより先に導出していた）．一次波 ψ₀ と，一つの回折波 ψ_h 以外の影響を無視できれば次のような連立微分方程式が得られる．これを「高木‐トーパンの式」という．

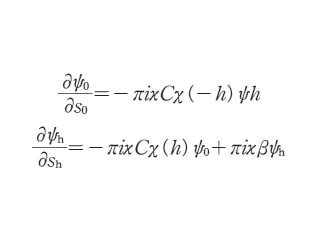
ここで s₀，s_h はそれぞれ両波の進行方向にとった斜行座標，κ は波数，C はX線の場合には偏極因子，電子線の場合には1である．β は入射波のブラッグ条件＊からの偏倚を表す係数，χ（－h），χ（h）は散乱ポテンシャルのフーリエ項を表す．完全結晶であれば，β，χ（－h），χ（h） は定数である．

出典　朝倉書店