コンコイド（読み）こんこいど（英語表記）conchoid

日本大百科全書(ニッポニカ)

コンコイド
こんこいど
conchoid

平面曲線の一つ。曲線Cが極座標を用いてr＝f(θ)と表されているとき、bを一つの定数として、r＝f(θ)＋bによって表される曲線C′を、Cの、極0に関するコンコイドという。

　曲線Cとして、直線r＝a secθをとった場合をニコメデスのコンコイドという。bの値によって、いろいろな形の曲線になる。これは、直交座標系では、
　　(x－a)²(x²＋y²)＝b²x²
と表される。

　曲線Cとして、円r＝a cosθをとったものをリマソン（蝸牛線(かぎゅうせん)）という。

［竹之内脩］

[参照項目] | リマソン

コンコイド

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

コンコイド
concoid

→曲線

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のコンコイドの言及

【曲線】より

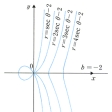
…原点Oと点A(a,0)を結ぶ線分を直径とする円を考え，この円周上の動点Qに対し，直線OQと直線x＝aとの交点をRとして，線分OQ上に点PをOPとQRの長さが等しくなるようにとれば，Pはこの曲線を描く。(2)方程式(x－a)²(x²＋y²)＝b²x²(a,bは正の定数)で表される四次曲線をコンコイドconchoidまたは螺獅（らし）線という(図6)。直線x＝a上の動点Qに対し，直線OQ上に長さbの線分QPをQの両側にとれば，Pはこの曲線を描く。…

【リンク装置】より

…また，機構の製作精度を高めることにより運動を正確に伝えることもできるので，その利用範囲は非常に広い。　リンク装置の古い利用例としては，コンコイド曲線の発見者のニコメデスNikomedesによるものがある(前2世紀ころ)。コンコイドとは図1のように定規B上の点Cが，定規Aの溝に沿って動くとき，定規Bの先端Pが描く曲線のことである。…

※「コンコイド」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」