精選版 日本国語大辞典 「極座標」の意味・読み・例文・類語
きょく‐ざひょう‥ザヘウ【極座標】
日本大百科全書(ニッポニカ) 「極座標」の意味・わかりやすい解説
極座標
きょくざひょう
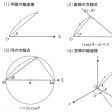
平面上の点を、定点Oからの距離rと定半直線OXからの偏角θとによって表す座標。Oを原点、OXを原線という。平面から原点Oを除いた部分と
{(r,θ) | 0<r, 0≦θ<2π}
とが一対一に対応するから、厳密には極座標は平面全体の座標系ではなく、平面から1点を除いた部分における座標系である。直交座標(x,y)と極座標(r,θ)との間には、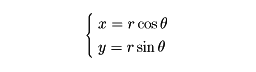
なる関係が成り立つ。極座標では原点Oを通らない直線の方程式はrcos(θ-α)=pで与えられる(αとpは定数)。また、原点を通る直線の方程式はθ=q(qは定数)で与えられる。原点を中心とする半径aの円の方程式はr=aで、また、原線上に中心をもち原点を通る半径aの円の方程式はr=2acosθである。極座標が(r1,θ1),(r2,θ2)である2点間の距離は、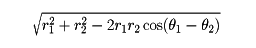
である。
空間の点を(r,θ, )で表すことができる。この(r,θ,
)で表すことができる。この(r,θ, )を空間の極座標といい、Oを原点という。空間からz軸を除いた部分と
)を空間の極座標といい、Oを原点という。空間からz軸を除いた部分と
{(r,θ, ) | 0<r, -π/2<θ<π/2, 0≦
) | 0<r, -π/2<θ<π/2, 0≦ <2π}
<2π}
とが1対1に対応するから、厳密には極座標は空間全体の座標系ではなく、空間から一直線を除いた部分における座標系である。直交座標(x,y,z)と極座標(r,θ, )との間には、
)との間には、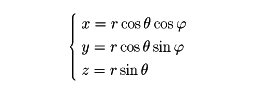
なる関係が成り立つ。
[荻上紘一]
百科事典マイペディア 「極座標」の意味・わかりやすい解説
極座標【きょくざひょう】
→関連項目円柱座標
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「極座標」の意味・わかりやすい解説
極座標
きょくざひょう
polar coordinates
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「極座標」の意味・わかりやすい解説
極座標 (きょくざひょう)
→座標
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
世界大百科事典(旧版)内の極座標の言及
【座標】より
…直交座標が(a,b,c),(a′,b′,c′)である2点間の距離は,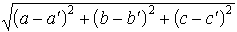 である。
である。
[極座標polar coordinates]
平面上に1点OとOからでる半直線OXを定めるとき,この平面上の点Pの位置は,線分OPの長さrと半直線OPの半直線OXからの角θによって表される。(r,θ)をPの極座標といい,rを動径,θを偏角という。…
※「極座標」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...