シュワルツの不等式（読み）シュワルツのふとうしき（その他表記）Schwarz's inequality

ブリタニカ国際大百科事典 小項目事典

シュワルツの不等式
シュワルツのふとうしき
Schwarz's inequality

コーシー＝シュワルツの不等式，ブニヤコフスキーの不等式ともいう。数列 a₁，a₂，…，a_n および b₁，b₂，…，b_n があるとき，不等式
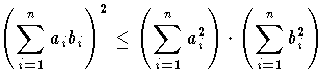が成り立つ。これをシュワルツの不等式という。等号は a₁/b₁＝a₂/b₂＝…＝a_n/b_n のときに成り立つ。この不等式は積分にも拡張される。 f(x) ，g(x) が区間 [a，b] で積分可能ならば
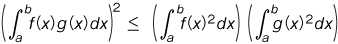が成り立つ。等号が成り立つのは，f(x) ，g(x) の比が定数であるとき，すなわち [a，b] において常に λ₁f(x)＋λ₂g(x)＝0 になるような定数が λ₁≠0 ，λ₂≠0 で存在するときだけである。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のシュワルツの不等式の言及

【絶対不等式】より

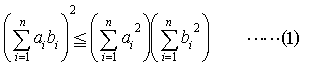…平面上の二つのベクトルa＝(a₁,a₂)，b＝(b₁,b₂)のなす角をθとすると，cosθ＝(a，b)/｜a｜･｜b｜(分子はベクトルの内積，分母はベクトルの長さの積)だから，｜cosθ｜≦1なることにより次の不等式が得られる。　(a₁b₁＋a₂b₂)²≦(a₁²＋a₂²)(b₁²＋b₂²)n次元のベクトルについても，同様にして，これをコーシー=シュワルツの不等式という。また，ベクトルの長さに関してよく知られた関係｜a＋b｜≦｜a｜＋｜b｜を成分で表したものをn次元のベクトルについて書けば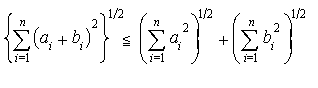，さらに一般に，任意のp≧1に対して，不等式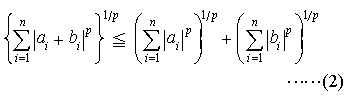，が成立する。…

※「シュワルツの不等式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」