精選版 日本国語大辞典 「不等式」の意味・読み・例文・類語
ふとう‐しき【不等式】
- 〘 名詞 〙 二つの数または式を不等号で結びつけたもの。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
日本大百科全書(ニッポニカ) 「不等式」の意味・わかりやすい解説
不等式
ふとうしき
数や式の大小関係を示す記号>,<,≧,≦を不等号といい、不等号を用いて表した式を不等式という。不等式は、実数の大小関係が基本になっている。したがって、不等式を扱うときは、かならず実数の範囲内で考えることにする。
a>b ⇔ a-b>0
a>b ⇔ 数直線上ではaはbの右側の点
が、不等号の基本の意味である(⇔は必要十分条件であることを示す)。
不等式の基本性質は
(1)a>0,b>0ならばa+b>0
a<0,b<0ならばa+b<0
(2)a>0,b>0またはa<0,b<0ならばab>0
a>0,b<0またはa<0,b>0ならば ab<0
(3)a>b,b>cならばa>c
(4)a>bならばa+c>b+c,a-c>b-c
(5)a>b,c>0ならばac>bc,a/c>b/c
a>b,c<0ならばac<bc,a/c<b/c
不等式の解法は
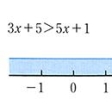
〔1〕一次不等式の場合、基本性質を利用して、x>a,x≧a,x<a,x≦aの形に帰着させる。たとえば、3x+5>5x+1の解は、
(3x+5)-5x-5>(5x+1)-5x-5(基本性質(4))
-2x>-4, x<2(基本性質(5))
こうしてx<2を得る()。
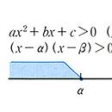
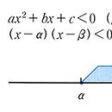
〔2〕二次不等式の場合、
ax2+bx+c⋛0 (a>0)
の形に整理してから、ax2+bx+c=0の解を考える。この解の状況によって、のように分類される。
〔3〕高次不等式の場合、因数分解して、因数の符号を考えて処理する。たとえば、
x3-2x2-5x+6>0の左辺は(x-1)(x+2)(x-3)と因数分解される。の符号の分析により、不等式の解は
-2<x<1, 3<xとなる()。
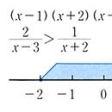
〔4〕分数不等式の場合、すべての項を一辺に集めて通分し、因数の符号を考えて処理する。たとえば、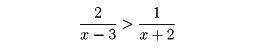
これを移項して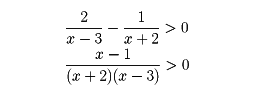
この最後の不等式の各因子の符号の分析は例2と同じく、のようになる。ゆえに、解は
-2<x<1, 3<x
となる()。
〔5〕このほか、無理式を含む不等式、指数関数、対数関数、三角関数を含む不等式など、さまざまな不等式がある。
不等式の解法では、不等式が正しいために不等式の中に含まれる文字がとりうる値の集合を求めた。これに対して、与えられた条件を満たすすべての文字の値の組合せについて、不等式が恒等的に成立することの証明が必要となる場合もある。たとえば、
a>0,b>0のときa3+b3≧a2b+ab2
を証明するには、
a3+b3-a2b-ab2
=(a+b)(a2-ab+b2-ab)
=(a+b)(a-b)2≧0
同様に
a2+b2+c2≧ab+bc+ca
を証明するには、
a2+b2+c2-ab-bc-ca=(1/2){(a-b)2+(b-c)2+(c-a)2}≧0
このような、文字がどのような実数値(あるいは正の実数値)をとっても成立するものは、絶対不等式とよばれる()。
[竹之内脩]
改訂新版 世界大百科事典 「不等式」の意味・わかりやすい解説
不等式 (ふとうしき)
inequality
二つの数学的対象A,Bが等しくないことを表すA≠B,AがBより大きいことを表すA>B,AがBより小さいかまたはAとBとが等しいことを表すA≦Bなどを不等式という。A>BとB<Aとは同じことを表す。AとBとの不等式が考えられ,それらが計算の対象となるのは,A,Bなどのとる値が実数のように大小関係の定められた集合の元であって,それらの元の間に加減乗除の算法が定まっているときである。例えば複素数には大小関係が定められないから,複素数についての不等式は扱われない。
実数の間に大小関係が定まり,実数についての不等式が考えられるのは,実数の次の性質による。
(1)二つの実数a,bの間にはa=b,a<b,a>bという三つの関係のうち,いずれか一つが必ず成り立つ。
(2)a>0なる実数aを正数と呼ぶとき,二つの正数の和および積は正数である。
これから,二つの実数a,bの大小は,a-b>0のときa>b,a-b<0のときa<bと定める。このとき,a>bかつb>cならばa>cなることが導かれる(a>b,b>cからそれぞれa-b>0,b-c>0となるから,(2)によって(a-b)+(b-c)>0,すなわちa-c>0となり,a>cを得る)。同様にして,a>b,c≧dならばa+c>b+d,とくにa+b>cならばa>c-bが成り立つ。すなわち,等式と同様に移項することができる。a>bのとき,c>0ならばac>bc,c<0ならばac<bc。a>b>0ならば1/a<1/b。a≧b>0,c≧d>0ならばac≧bdなどのような不等式の基本的性質は,すべて(1),(2)から導かれる。
文字a,b,……に関する不等式が,それらの文字にあらかじめ定められた範囲の値を与えたときつねに成立する場合に,その不等式を絶対不等式という。a2≧0はすべての実数aに対して成立し,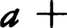
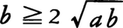 はすべての正数a,bに対して成立する絶対不等式である。これに対して,文字x,y,……に関する不等式が,それらの文字にどのような値を与えたとき成立するかを問題にするとき,その不等式を条件付き不等式(条件不等式ともいう)という。条件付き不等式が成立するようなx,y,……の値の範囲をその不等式の解といい,解を求めることを不等式を解くという。例えば不等式,
はすべての正数a,bに対して成立する絶対不等式である。これに対して,文字x,y,……に関する不等式が,それらの文字にどのような値を与えたとき成立するかを問題にするとき,その不等式を条件付き不等式(条件不等式ともいう)という。条件付き不等式が成立するようなx,y,……の値の範囲をその不等式の解といい,解を求めることを不等式を解くという。例えば不等式,
(x-2)(x-3)>0の解は
x<2とx>3
(x-2)(x-3)<0の解は2<x<3
(x-2)(x-3)(x-4)>0の解は
2<x<3とx>4
である。二つの文字x,yについての不等式f(x,y)>0,またはf(x,y)<0の解は,これらの不等式を満たすx,yの値を座標とする点の集合として図示されて,それぞれ関数f(x,y)の正領域または負領域と呼ばれる。f(x,y)がx,yの連続関数ならば,正領域と負領域との境界上ではf(x,y)=0となる。
二つ以上の条件付き不等式を組にしたものを連立不等式という。一つの文字xに関する連立不等式の解は,おのおのの不等式の解の共通部分をとればよい。例えば連立不等式,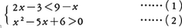
の解は,(1)の解と(2)の解の共通部分を求めて,x<2,3<x<4となる(図1)。二つの文字x,yに関する連立不等式の解は,おのおのの不等式を満たす平面上の点(x,y)の集合の共通部分である。例えば連立不等式,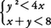
の解は図2の重なった部分である(境界線上は含まない)。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「不等式」の意味・わかりやすい解説
不等式
ふとうしき
inequality
(1) a>b(a はb より大きい)
(2) a≧b(a はb より大きいかまたは等しい)
(3) a<b(a はb より小さい)
(4) a≦b(a はb より小さいかまたは等しい)
ある変数についての不等式が与えられたとき,不等式を満たすような変数の値全体の集合を不等式の解と呼ぶ。また不等式の解を求めることを,不等式を解くという。不等号を含んだ数式が変数の 1次式であるとき,特にその不等式を 1次不等式と呼ぶ。不等式の両辺に同じ実数を加えても,不等号は変わらない。この性質を用いて,不等式を解く際に,等式と同様に移項の操作をすることができる。不等式の両辺に正数を掛けたり割ったりしても不等号は変わらないが,両辺に負数を掛けたり割ったりすると不等号の向きが反対になる。実数の大小に関する不等式は次の性質をもつ。
(1) a≦a,a≧a
(2) a≧b かつ a≦b ならば a=b
(3) a≦b かつ b≦c ならば a≦c
これらは順序の公理として,抽象的に定式化される性質である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...