円や放物線と直線で囲まれた平面図形の面積を求めることは,ギリシア時代から知られていたが,これらをもっと一般に,系統的に扱うのが積分法であって,その中心的概念が積分である。積分法は微分法とともに17世紀にI.ニュートンとG.W.ライプニッツによって発見された。積分は,曲線で囲まれた平面の部分の面積や,曲線の長さ,関数の平均値などの計算に用いられるばかりでなく,種々の物理量を定義し,計算するにも重要である。また積分法は微分法とともに自然科学,工学にも大きな影響を与えている。積分の考えは1変数の関数から一般に多変数の関数や複素変数の関数に拡張され,関数の大域的な性質を調べるのにも有用である。
積分演算は,微分演算の逆演算と密接に関連する。以下,本項ではまず面積を求める方法としての積分の定義を与え,微分演算との関係を述べ,積分の性質や計算法およびその関連事項などを述べる。
定積分と不定積分
a≦x≦bなるxの範囲(これを区間[a,b]という)で与えられた関数f(x)があるとき,この区間を,
a=x0<x1<x2<……<xn-1<xn=b
なる分点xjでn個の小区間に分け,それぞれの小区間[xj-1,xj](j=1,……,n)の長さxj-xj-1に,その区間内の任意の点ξjにおける関数値f(ξj)を掛けて加えた和,
f(ξ1)(x1-x0)+f(ξ2)(x2-x1)+……+f(ξn)(xn-xn-1) ……(1)
を考える。どの小区間の長さも限りなく小さくなるように分点の数を限りなく増していくとき,この和が,分点やξjのとり方に無関係な一定の値Sに限りなく近づくならば,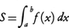 と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。
と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。
また,区間[a,b]をその積分区間といい,a,bをそれぞれ積分区間の下端,上端という。
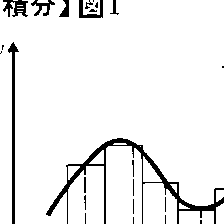
関数f(x)が区間[a,b]で連続ならば,f(x)はこの区間で定積分をもつ,すなわち積分可能であることが証明されている。ただし,f(x)が[a,b]で連続とは,素朴な概念で説明するならば,この区間でy=f(x)のグラフが一つの連続した(切れめのない)曲線になることである。とくに,区間[a,b]においてf(x)≧0ならば,この定積分の値はy=f(x)のグラフとx軸および直線x=a,x=bで囲まれた部分の面積に等しい(図1)。いまy=f(x)のグラフと,x軸および直線x=x1,x=x2で囲まれた部分の面積をSf(x1,x2)と書くことにする。ただしx1≦x2とし,x1=x2のときにはSf(x1,x2)=0とする。Sf(a,b)は上に述べた定積分の値Sに等しい(図2)。a≦x≦bなるxに対してφ(x)=Sf(a,x)とおくと,a<x<bのとき,x<x+h<bとなるh>0に対してφ(x+h)-φ(x)=Sf(x,x+h)である。fはxにおいて連続であるから,h→0のときf(x+h)→f(x)。よって,fの[x,x+h]における最大値,最小値をそれぞれM(h),m(h)とすると,x≦t≦x+hのときm(h)≦f(t)≦M(h)であって,h→0のときm(h)→f(x),M(h)→f(x)となる。このとき,Sf(x,x+h)は図3の二つの長方形ABDC,ABFEの面積にはさまれて,hm(h)≦Sf(x,x+h)≦hM(h)。正数hで割ってh→0とすると両端辺がf(x)に近づくから{φ(x+h)-φ(x)}/h→f(x)となる。h<0のときも同様に考えられる。x=aあるいはx=bでは,それぞれh>0,h<0の場合だけを考えることにする。以上により区間[a,b]でφ′(x)=f(x)となることがわかる。fが[a,b]で定義された一般の(f≧0と限らない)連続関数のときは,g(x)=f(x)+c≧0となるような定数c≧0をとり,gを今までのfと考えると,φ′(x)=g(x)=f(x)+cとなる関数φがある。よってF(x)=φ(x)-cxとおけば,F′(x)=f(x)となる。このように,与えられた区間で連続な任意の関数fに対して,それを導関数とする関数Fが存在する。この関数Fをもとの関数fの原始関数という。このときFに定数を加えても同じfの原始関数であるが,逆にfの任意の原始関数Gに対して(G-F)′=f-f=0となるから,G-Fはある定数Cに等しい。すなわちG(x)=F(x)+C。この形の関数を関数fの不定積分といい,記号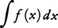 で表す。すなわち,F′(x)=f(x)のとき,
で表す。すなわち,F′(x)=f(x)のとき,
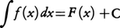
このときfを被積分関数,xを積分変数,Cを積分定数という。また,関数fからその不定積分を求めることを,f(x)を積分するという。なお,不定積分という言葉は原始関数と同意義に用いられることもある。ここで,もとのf≧0なる連続関数fの場合に面積S=Sf(a,b)を求める問題を再考しよう。fの一つの原始関数Fを知れば,
Sf(a,x)=F(x)+C (Cは定数)
だから,x=b,x=aとおいて,
Sf(a,b)=F(b)+C
0=Sf(a,a)=F(a)+C
したがってSf(a,b)=F(b)-F(a)となる。Sf(a,b)は前述の定積分の値だから,
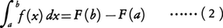
この式はf≧0という仮定がなくても成り立つことが次のようにしてわかる。前のようにg(x)=f(x)+C≧0となるような定数C≧0をとり,fをgで置き換えると,Fはφ(x)=F(x)+cxで置き換えられ,(2)は,
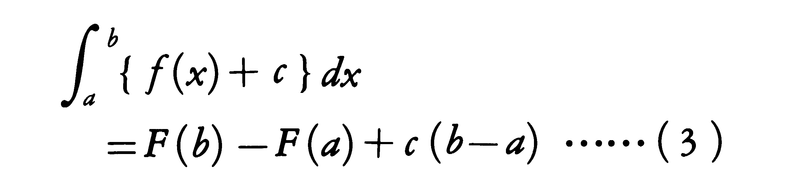
となる。ところが,定積分が(1)の形の和の極限として定義されていることにより,
(3)の左辺=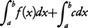
=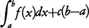
となるから,(3)の両辺からc(b-a)を引くことにより,(2)の形の式が(f≧0の仮定なしに)得られたことになる。関数fの原始関数は定数の差を除いて定まるから,(2)の右辺の値は,fの原始関数Fの選び方に関係しないことに注意しなければならない。(2)を微分積分法の基本定理という。
不定積分の基本性質と計算法
与えられた関数の不定積分を求めることを,その関数を積分するという。そのために,すでに知られている関数の組合せで計算する方法が積分法であって,微分法の逆演算にあたる。
微積分学でおもな対象とする関数は,いわゆる初等関数,すなわち代数関数,指数関数,対数関数,三角関数,逆三角関数およびそれらの合成関数を作る操作を有限回行って得られる関数である。初等関数を微分すると必ず初等関数になるが,初等関数を積分すると必ずしも初等関数にならないので,初等関数の範囲で積分法がいつでもできるとは限らない。例えば,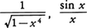 のような簡単な初等関数でも,その原始関数は初等関数でないことが証明される。不定積分を計算するには,いくつかの簡単な関数の不定積分を知って,もっと複雑な関数の積分をこれに帰着させる。その変形には次の基本公式が用いられる。ただし不定積分を含む等式は,定数の差を除いて成り立つのである。
のような簡単な初等関数でも,その原始関数は初等関数でないことが証明される。不定積分を計算するには,いくつかの簡単な関数の不定積分を知って,もっと複雑な関数の積分をこれに帰着させる。その変形には次の基本公式が用いられる。ただし不定積分を含む等式は,定数の差を除いて成り立つのである。
(1)線形性 α,βを定数とするとき,
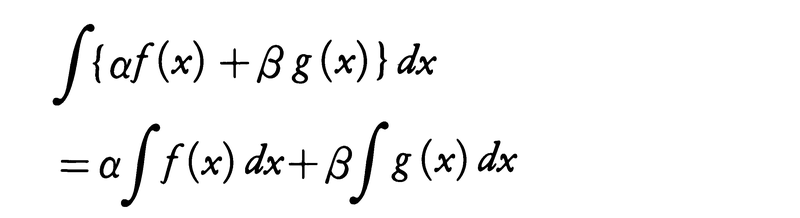
(2)部分積分法 f,f′,g,g′が連続ならば,
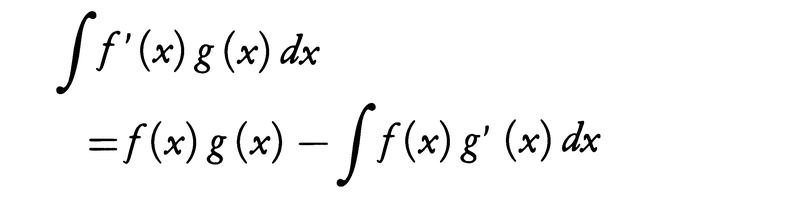
(3)置換積分法
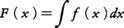
においてx=φ(t)(ただし,φの値域はfの定義域に含まれ,φ′は連続とする)とおくと,
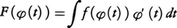
とくにφが狭義単調ならば,連続な逆関数φ⁻1が定まり,上の式の右辺を計算してからt=φ⁻1(x)を代入して,f(x)の原始関数F(x)が求められる。
次に初等関数の不定積分を与える公式のおもなものを表に列挙する。
有理関数を積分するには,有理関数を整式と既約真分数式の和で表し,分数式の分母を一次式と二次式の因数に分けて部分分数に分解すると,初等関数の範囲で積分できる。
定積分の性質と計算法
定積分の定義から次の各性質が導かれる。
(1)線形性 α,βを定数とすると,
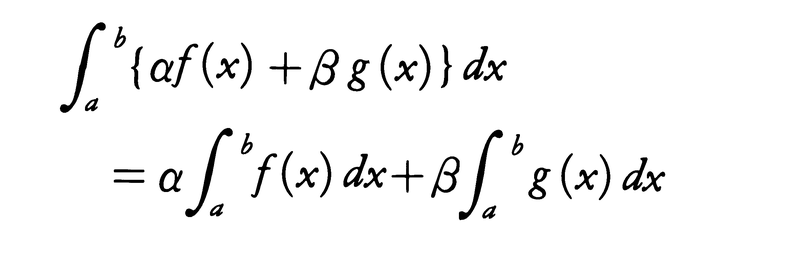
(2)単調性 f(x)≧g(x)ならば,
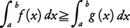
(3)区間に関する加法性 a<c<bならば,
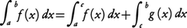
(4)積分の平均値の定理 fが区間[a,b]で連続ならば,
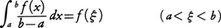
となるξが存在する。
区間に関する加法性(3)がa,b,cの大きさの順に関係なく成り立つようにするため,b≦aのときの積分,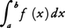 を次のように定める。
を次のように定める。
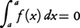
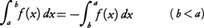
こうすると,(3)はa,b,cの大きさの順に関係なく成立するが,(2)はb<aのときには不等号の向きが反対になる。
不定積分の部分積分法,置換積分法と(2)とから,定積分の部分積分法,置換積分法が導かれる。
(5)部分積分法 f,f′,g,g′が閉区間[a,b]において連続ならば,
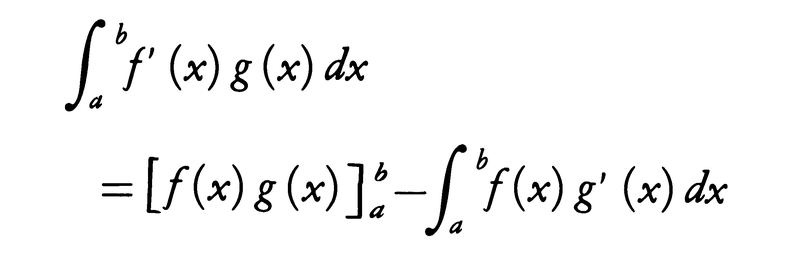
ただし,一般に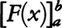 はF(b)-F(a)を表す。
はF(b)-F(a)を表す。
(6)置換積分法 区間[α,β]でφ(t)が単調,φ′(t)が連続であって,tがαからβまで動くとき,x=φ(t)がaからbまで変化するならば,
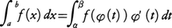
f(x)が有限閉区間でない区間において連続である場合にも,その区間における定積分を有限閉区間における定積分の極限として定義することができる。例えばfがa≦x<bで連続な場合には,a<b′<bなるb′をとりb′→bとするとき極限値,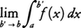 が存在するならば,その値を,
が存在するならば,その値を,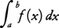 と定める。区間a<x≦b,あるいはa<x<bにおける積分も同様にして定義する。例えば,0<α<1のとき,
と定める。区間a<x≦b,あるいはa<x<bにおける積分も同様にして定義する。例えば,0<α<1のとき,
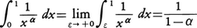
また,無限区間a≦x<∞における積分は,a<b<∞なるbをとってb→∞としたときの極限値,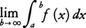 が存在するとき,その値を,
が存在するとき,その値を,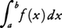 と定義する。他の形の無限区間の場合もこれにならって定義する。例えば,α>1のとき,
と定義する。他の形の無限区間の場合もこれにならって定義する。例えば,α>1のとき,
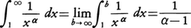
このように積分の定義を拡張しても,線形性,単調性,区間に関する加法性などはすべて成立する。区間内に関数fの有限個の不連続点がある場合には,それらの不連続点で初めの区間を有限個の小区間に分け,それぞれの小区間のうえで上のように積分を定めて加えればよい。
与えられた関数が連続な区間では,その原始関数がわかれば(2)によって定積分が計算されるから,定積分の計算は不定積分の計算に帰着されるが,不定積分が求められなくても,特別な区間の定積分が計算できる場合がある。例えば,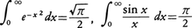 などは代表的なものである。
などは代表的なものである。
多変数の関数の積分
2変数の関数の積分の定義を述べるが,一般の多変数の場合も同様である。xy平面上の有界集合Eで定義された関数f(x,y)があるとき,Eを含む長方形K:a≦x≦b,c≦y≦dをとり,
a=x0<x1<x2<……<xm=b
c=y0<y1<y2<……<yn=d
なる分点xi,yjにより,Kをmn個の小さい長方形Kij:xi-1≦x≦xi,yj-1≦y≦yjに分割する。また(x,y)∈K-Eに対しては,f(x,y)=0として関数fの定義域をKまで拡張しておく。各Kijの中に任意の点(ξij,ηij)をとり,1変数の場合の(1)と同様に,
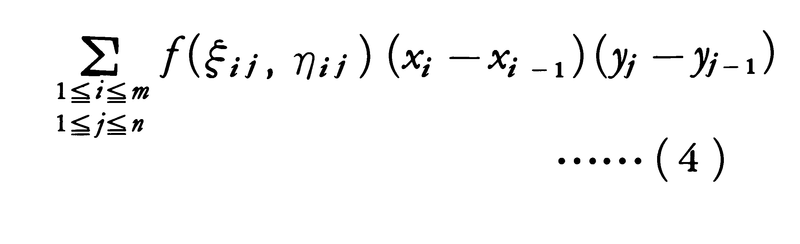
を考える。xi-xi-1,yj-yj-1の最大値が0に近づくように分点を増していくとき,(4)の値が分点xi,yjや点(ξij,ηij)のとり方に無関係な一定の値Sに限りなく近づくならば,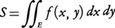 と書いて,これを関数fのEにおける二重積分,または単に積分という。これに対して,前に述べた1変数の積分を単積分と呼ぶことがある。上のような極限値Sの存在およびその値は,Eを含む長方形Kのとり方には関係しない。とくにf(x,y)≡1として上の積分が定まるとき,Eは面積確定であるといい,その値をEの面積という。例えば,有限個のなめらかな曲線(x=φ(t),y=ψ(t),a≦t≦bと表したときに,φ′(t),ψ′(t)が連続であるような曲線)で囲まれた図形は面積確定である。また,区間a≦x≦bでφ(x),ψ(x)が連続であってφ(x)≦ψ(x)なるとき,
と書いて,これを関数fのEにおける二重積分,または単に積分という。これに対して,前に述べた1変数の積分を単積分と呼ぶことがある。上のような極限値Sの存在およびその値は,Eを含む長方形Kのとり方には関係しない。とくにf(x,y)≡1として上の積分が定まるとき,Eは面積確定であるといい,その値をEの面積という。例えば,有限個のなめらかな曲線(x=φ(t),y=ψ(t),a≦t≦bと表したときに,φ′(t),ψ′(t)が連続であるような曲線)で囲まれた図形は面積確定である。また,区間a≦x≦bでφ(x),ψ(x)が連続であってφ(x)≦ψ(x)なるとき,
a≦x≦b,φ(x)≦y≦ψ(x) ……(5)
で定義される図形Eは面積確定である。面積確定の閉集合Eで連続な関数f(x,y)に対しては,Eにおける積分が存在する。なお,2変数(一般に多変数)の関数の積分を簡単に,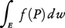 のように書くこともある。連続関数の二重積分の計算は単積分の計算に帰着される。例えば,(5)で定義される図形Eでf(x,y)が連続ならば,まず,
のように書くこともある。連続関数の二重積分の計算は単積分の計算に帰着される。例えば,(5)で定義される図形Eでf(x,y)が連続ならば,まず,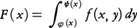 はxの連続関数となり,
はxの連続関数となり,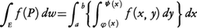 が成り立つ。この右辺を次のようにも書く。
が成り立つ。この右辺を次のようにも書く。
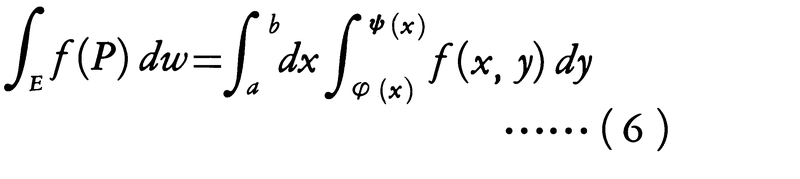
3変数の関数の積分(三重積分),一般に多変数の関数の積分(多重積分)についても,以上と同様のことがいえる。例えば三重積分の場合,(6)に相当する事実は,a≦x≦b,φ1(x)≦y≦φ2(x),ψ1(x,y)≦z≦ψ2(x,y)で定義される三次元の点集合Eにおいて,f(x,y,z)が連続ならば,
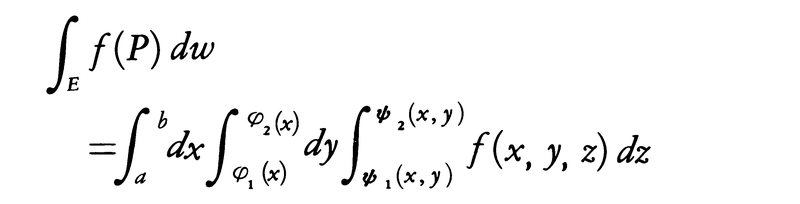
単積分の場合の置換積分法に相当するものとして,重積分の場合には次の変数変換の公式がある。x=φ(u,v),y=ψ(u,v)により,uv平面上の点集合Bからxy平面上の点集合Aへの1対1の写像が与えられていて,φ,ψはu,vに関して連続偏微分可能とする。このとき,
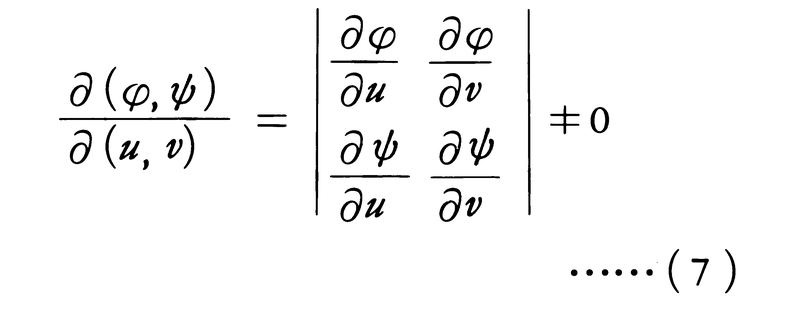
とすると,A,Bのうち一方が面積確定なら他方も面積確定で,
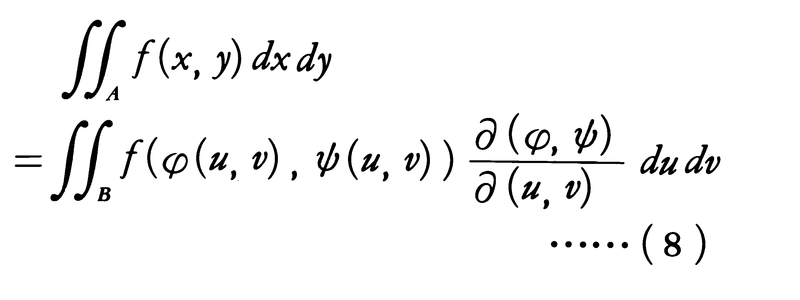
(7)の行列式を関数行列式,またはヤコビの行列式(ヤコビアンJacobian)という。とくに,x=r cosθ,y=r sinθ(二次元の極座標)とすると,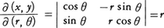 であるから,
であるから,
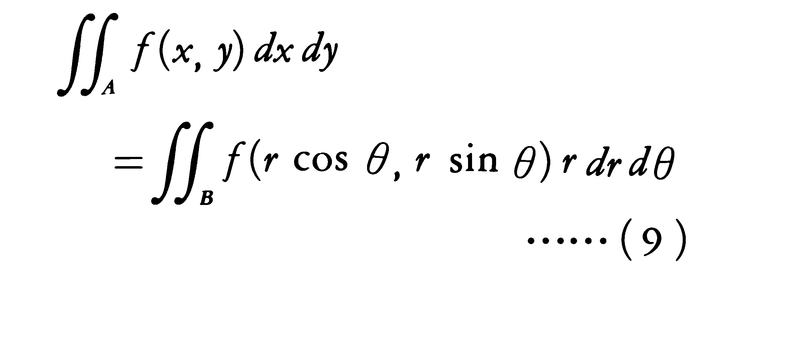
三次元の場合にはx=φ(u,v,w),y=ψ(u,v,w),z=χ(u,v,w)について上と同様な仮定のもとに,関数行列式,
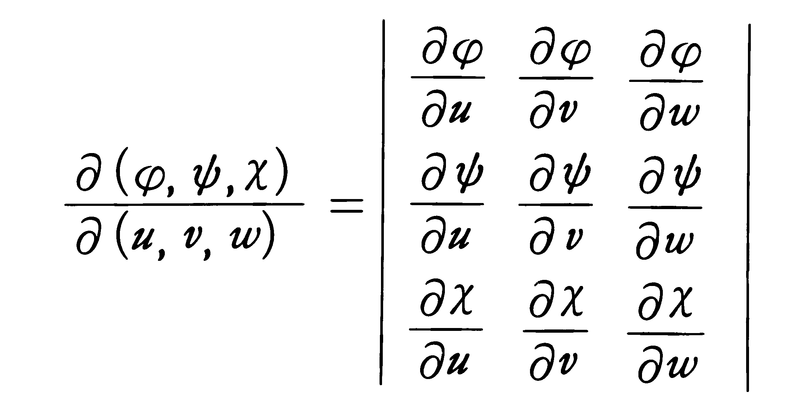
を用いて(8)と同様な公式を書くことができる。とくにx=rsinθcosφ,y=rsinθsinφ,z=rcosθ(三次元の極座標)の場合は,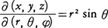 となるから,(9)と同様な次の公式を得る。
となるから,(9)と同様な次の公式を得る。
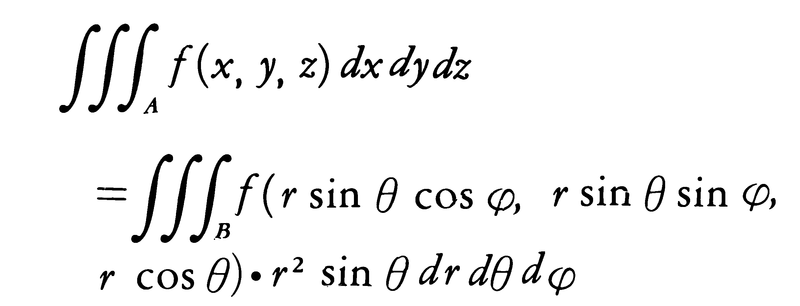
→区分求積法 →積分論 →線積分 →体積分 →面積分 →リーマン積分 →ルベーグ積分
執筆者:伊藤 清三


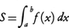 と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。
と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。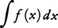 で表す。すなわち,F′(x)=f(x)のとき,
で表す。すなわち,F′(x)=f(x)のとき,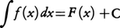
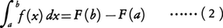
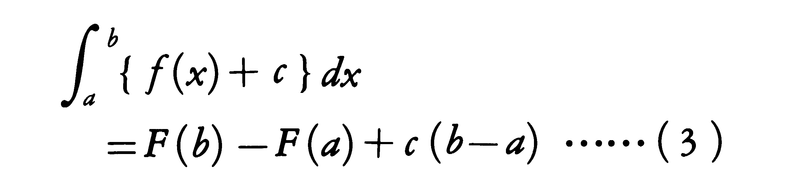
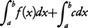
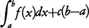
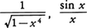 のような簡単な初等関数でも,その原始関数は初等関数でないことが証明される。不定積分を計算するには,いくつかの簡単な関数の不定積分を知って,もっと複雑な関数の積分をこれに帰着させる。その変形には次の基本公式が用いられる。ただし不定積分を含む等式は,定数の差を除いて成り立つのである。
のような簡単な初等関数でも,その原始関数は初等関数でないことが証明される。不定積分を計算するには,いくつかの簡単な関数の不定積分を知って,もっと複雑な関数の積分をこれに帰着させる。その変形には次の基本公式が用いられる。ただし不定積分を含む等式は,定数の差を除いて成り立つのである。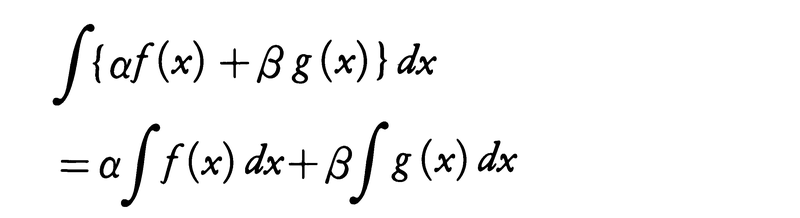
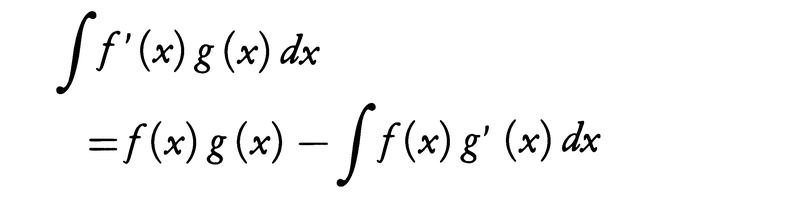
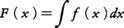
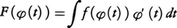
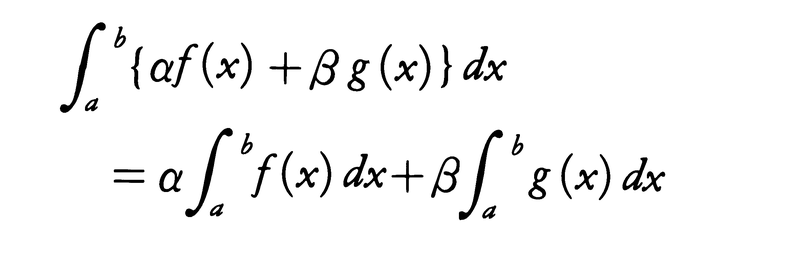
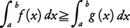
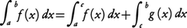
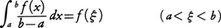
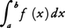 を次のように定める。
を次のように定める。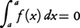
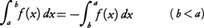
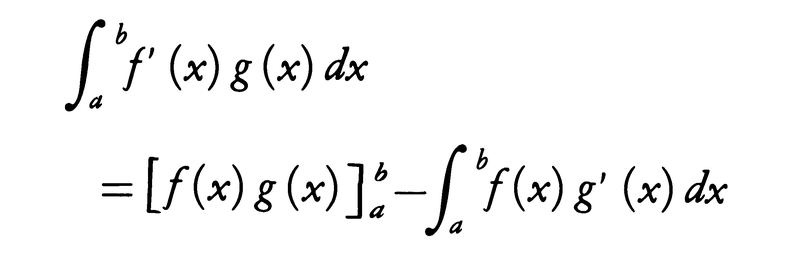
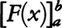 はF(b)-F(a)を表す。
はF(b)-F(a)を表す。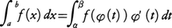
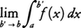 が存在するならば,その値を,
が存在するならば,その値を,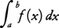 と定める。区間a<x≦b,あるいはa<x<bにおける積分も同様にして定義する。例えば,0<α<1のとき,
と定める。区間a<x≦b,あるいはa<x<bにおける積分も同様にして定義する。例えば,0<α<1のとき,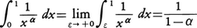
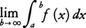 が存在するとき,その値を,
が存在するとき,その値を,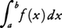 と定義する。他の形の無限区間の場合もこれにならって定義する。例えば,α>1のとき,
と定義する。他の形の無限区間の場合もこれにならって定義する。例えば,α>1のとき,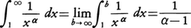
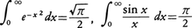 などは代表的なものである。
などは代表的なものである。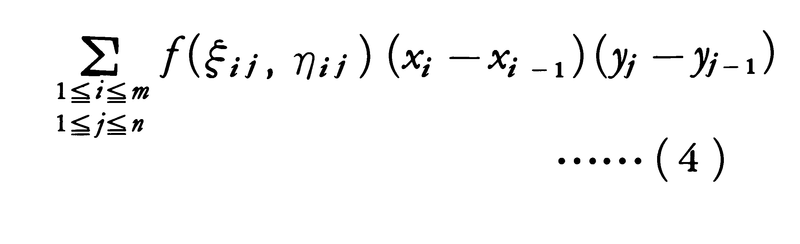
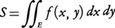 と書いて,これを関数fのEにおける二
と書いて,これを関数fのEにおける二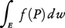 のように書くこともある。連続関数の二重積分の計算は単積分の計算に帰着される。例えば,(5)で定義される図形Eでf(x,y)が連続ならば,まず,
のように書くこともある。連続関数の二重積分の計算は単積分の計算に帰着される。例えば,(5)で定義される図形Eでf(x,y)が連続ならば,まず,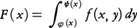 はxの連続関数となり,
はxの連続関数となり, が成り立つ。この右辺を次のようにも書く。
が成り立つ。この右辺を次のようにも書く。
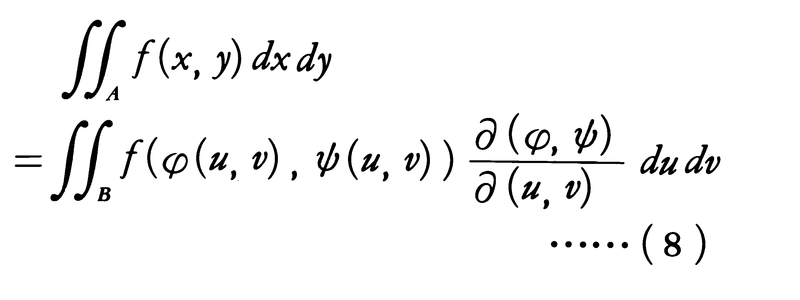
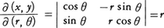 であるから,
であるから,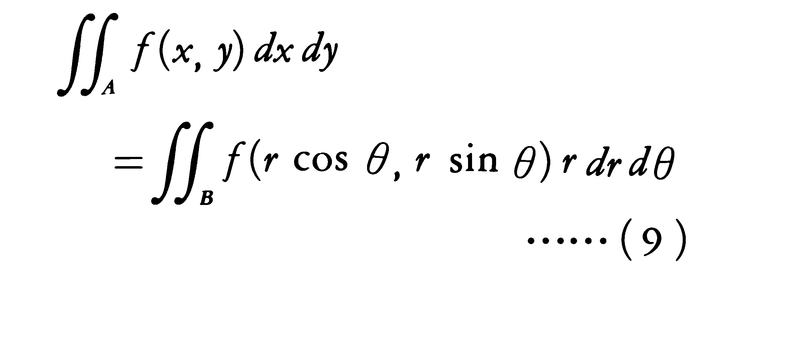
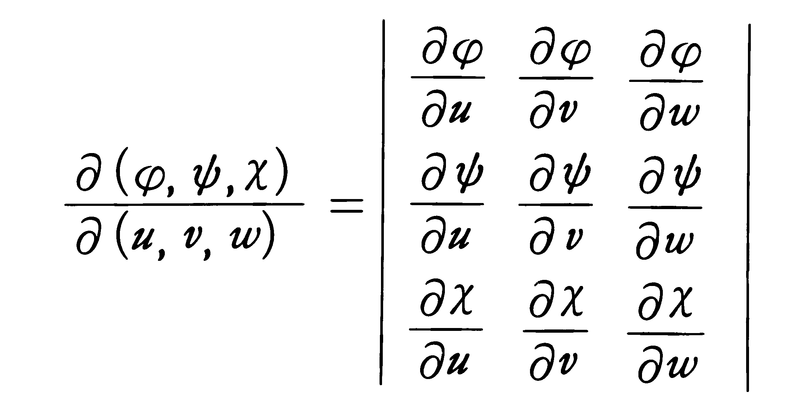
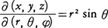 となるから,(9)と同様な次の公式を得る。
となるから,(9)と同様な次の公式を得る。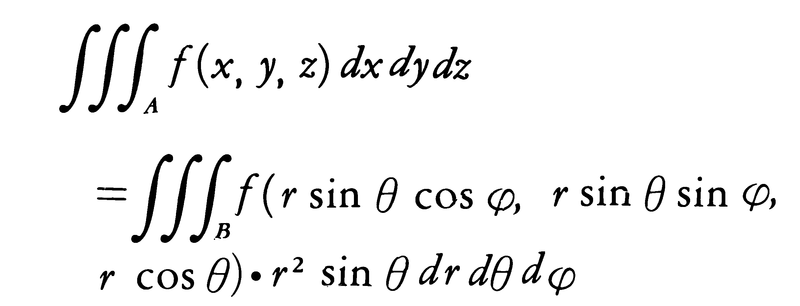
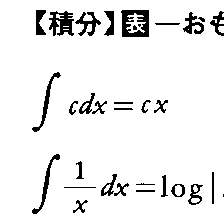
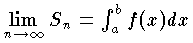 と書き,これを [a,b] における
と書き,これを [a,b] における