改訂新版 世界大百科事典 「マルチンゲール」の意味・わかりやすい解説
マルチンゲール
martingale
数学用語。公平な賭（かけ）という考えから導入された概念で，1950年ころから組織的に研究され，確率論の重要な一分野になっている。確率空間（Ω，
，P）上の増大情報系n（n＝0，1，……）に対し，確率変数列Xn（n＝0，1，……）が次の3条件，（Ⅰ）Xnはn-可測，（Ⅱ）E｜Xn｜＜∞，（Ⅲ）E（Xn+1/n）＝Xnをみたすとき，マルチンゲールという。とくに（Ⅲ）はマルチンゲール性と呼ばれ，これにより，E（Xn）はnに無関係になる。次の定理は有用である。
収束定理
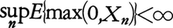ならば，Xnは概収束する。
ドゥーブの任意抽出定理
有界な停止時間の増大列τ0≦τ1≦……，に対し，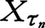
（n＝0，1，2，……）は，増大情報系
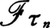に関するマルチンゲールとなる。例えば，（1）可積分なXに対し，nに関する条件つき平均値の列Xn＝E（X/n）（n≧0）はマルチンゲールである。（2）ξn（n≧0）は平均値0の独立確率変数列で各ξnがn-可測のとき部分和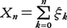
はマルチンゲールになる。
（Ⅲ）のE（Xn+1/n）＝Xnにおいて等号＝が≧に弱められたとき，劣マルチンゲール，≦のときは優マルチンゲールと呼ばれる。連続時間変数Xt（t≧0）の場合も同様に定義される。
執筆者：西尾 真喜子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報