リー環（読み）リーかん（英語表記）Lie ring; Lie algebra

ブリタニカ国際大百科事典小項目事典「リー環」の意味・わかりやすい解説

リー代数ともいう。一つの分配系 L の乗法を [a，b] で表わすとき

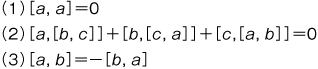が L に属する任意の a，b，c に対して成り立てば，L をリー環という。リー群から，微分作用素の代数としてつくられる。

出典　ブリタニカ国際大百科事典小項目事典ブリタニカ国際大百科事典小項目事典について　情報

地表面や大気層が熱を放射して冷却する現象。赤外放射による冷却。大気や地球の絶対温度は約 200～300Kの範囲内にあり，波長 3～100μm，最大強度の波長 10μmの放射線を出して冷却する。赤外放射...