リー群（読み）リーぐん（その他表記）Lie group

改訂新版　世界大百科事典

リー群 (リーぐん)
Lie group

行列式の値が0でないn次実行列の全体GL（n;R）は，行列A＝（a_ij）をn²次元ユークリッド空間R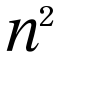の点（a₁₁，a₁₂，……，a_nn-1，a_nn）と同一視することにより，R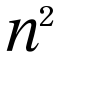の開集合となる。GL（n;R）は行列の積により群となるが，対応（A，B）→AB⁻¹による写像GL（n;R）×GL（n;R）→GL（n;R）は，GL（n;R）⊂R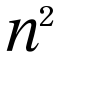とみるとき有理関数で表されるから，C^ω級写像（実解析写像）である。一般に，Gは群であると同時にC^ω級多様体で，対応（g，g′）→gg′⁻¹による写像G×G→GがC^ω級写像であるとき，Gをリー群といい，多様体としての次元がnのときGをn次元リー群という。GL（n;R）はn²次元リー群である。n次元リー群はまた次のようにも定義できる。Gは位相群で，その単位元eのある近傍Uからn次元ユークリッド空間Rⁿのある開集合Vの上への同相写像で次の条件をみたすものがとれるとき，Gをn次元リー群という。Uの元をそのVにおける像と同一視してRⁿの点で表すとき，Uの元x＝（x₁，……，x_n），y＝（y₁，……，y_n）に対し積xyがUに属せば，xy＝（z₁，……，z_n）としてz_i＝f_i（x₁，……，x_n，y₁，……，y_n）（i＝1，2，……，n）と表せるが，関数f₁，……，f_nは2n個の変数x₁，……，x_n，y₁，……，y_nのC^ω級関数である。このようにリー群は群乗法の定義に関数の解析性の条件を含んでいるので，その研究に微分方程式論などの解析学が活用できてくわしく研究されており，位相群のなかで重要な地位をしめている。回転群などの古典群はすべてリー群である。

　ベクトル空間Lにおいて，Lの任意の2元X，Yに対し［X，Y］で表されるLの元が定められていて，次の条件が成り立つとき，Lを（実数体上の）リー代数またはリー環という。（1）［X，Y］は双線型である。（2）［X，Y］＋［Y，X］＝0。（3）［X，［Y，Z］］＋［Y，［Z，X］］＋［Z，［X，Y］］＝0。リー群Gの単位元eにおける接ベクトルのつくるベクトル空間をL（G）とし，L（G）の2元X，Yに対しL（G）の元［X，Y］を次のように定義すれば，L（G）はリー代数となる。eを通る曲線x：（－α，α）→G（x（0）＝e）で（dx/dt）_t=0がXを表し，｜s｜，｜t｜，｜s＋t｜＜αならばx（s＋t）＝x（s）x（t）であるようなものをとり，Yについても同様な曲線y：（－β，β）→Gをとる。このとき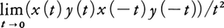，の表す接ベクトルを［X，Y］と定義する。L（G）をリー群Gのリー代数という。例えば，GL（n;R）のリー環は実n次行列全体のつくるベクトル空間において，回転群SO（n）のリー環は実n次歪対称行列全体のつくるベクトル空間において，ともに［X，Y］＝XY－YXと定義したものである。リー群の局所的性質は完全にリー代数の性質に帰着できる。リー群の理論は19世紀後半のS.リーの連続変換群の研究に始まり，20世紀に入ってE.カルタンとH.ワイルらの研究によって完成した。現代ではリー群は数学の種々の分野や理論物理学で広く活用されている。
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

リー群
りーぐん
Lie group

連結解析的多様体Gが同時に群であって、群の演算(g₁,g₂)→g₁g₂が積多様体G×GからGへの解析的写像で、さらに逆元をとる演算g→g^-1がGからGへの解析的写像であるとき、Gをリー群または解析的群という。

　このようにリー群は多様体と群の結合概念であるが、ノルウェーの数学者M・S・リーによって、幾何学や微分方程式を群論を用いて研究するため考え出されたもので、その名をとってリー群とよばれる。

　リー群Gは、実多様体か複素多様体かによって、それぞれ、実リー群、複素リー群ともいう。実数全体の加法群R、実一般線形群GL(n,R)は実リー群であり、複素数全体の加法群C、複素一般線形群GL(n,C)は複素リー群である。

　抽象的な群の場合と同じように、リー群の部分群、正規部分群、商群、準同型写像、同型写像などが、多様体としての自然な条件をあわせて考えて定義され、群論と類似のリー群論が完成されている。

　リー群論の特長は、リー群Gにリー代数ɡが、次に述べるように、自然に構成され、重要な役割を果たすところにある。

　リー群Gの元gに対し、解析的写像
　　Φ_g：G∋x→gx∈G
の微分dΦ_gは、Gの単位元eにおける接空間T(e)からgにおける接空間T(g)の上への線形空間の同型写像を与える。いま、X_e∈T(e)に対し、
　　X：G∋g→dΦ_g・(Xe)∈T(g)
で、多様体Gのベクトル場Xをつくる。このようなXの全体ɡ=｛X｜X_e∈T(e)｝はT(e)と同型な線形空間で、ベクトル場の積
　　〔X,Y〕=X・Y―Y・X
によって、一つの代数系となる。この代数ɡをL(G)と書き、リー群Gのリー代数という。

　リー群GL(n,R)のリー代数は、n次実正方行列環M_n(R)から行列の積の差XY―YX=〔X,Y〕で得られるリー代数ɡl(n,R)になる。

　任意のリー代数ɡに対し、L(G)=ɡになるようなリー群Gが存在する。

　リー群Gのリー部分群Hのリー代数L(H)はL(G)の部分リー代数になり、逆にL(G)のリー部分代数ηに対し、L(H)=ηになるGのリー部分群Hがただ一つ存在する。

　また、リー群G₁からリー群G₂への準同型写像fの微分dfは、L(G₁)からL(G₂)へのリー代数準同型写像になり、fはdfで決まる。

　以上は、主として連結リー群について述べたが、連結でない多様体であるリー群も考えられ、リー代数の理論とあわせて、リー群論として、完成された数学の一部門になっている。また近年、p進数体上でも多様体が考えられ、p進リー群論もつくられて、整数論などに応用されている。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

リー群
リーぐん
Lie groupe

位相群が微分多様体になっていて，群演算が微分可能なものをリー群という。変換群として微分概念の可能なものである。

出典　ブリタニカ国際大百科事典 小項目事典