コルテヴェク‐ドフリースの方程式（その他表記）Korteweg-de Vries equation

法則の辞典

コルテヴェク‐ドフリースの方程式【Korteweg-de Vries equation】

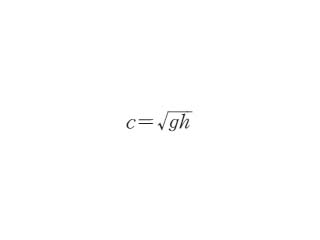一次元的な浅い水路に生じる波の記述のための方程式．略してKdV方程式＊ともいう．ソリトンと呼ばれる安定な解をもつ．波の振幅を a ，波長を λ，水深を h として，a/h～（h/λ）²≪1の条件が満たされた場合，x 方向に速さ （&scriptg; は重力加速度）で進む系からみたとき，水面の盛り上がり u は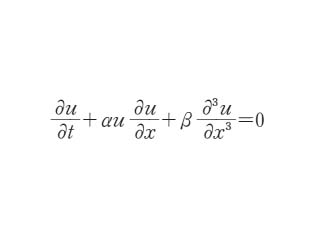

で記述できる．ここで α と β は c，h によって定まる定数である．この式から得られる解は，物理的には（αu&partial;u/&partial;x）なる非線形項による波の立上りの効果と，分散項 β（&partial;³u/&partial;x³）による波の広がりの効果の重畳した波となる．いくつかの解があるが，中でも最も重要なのは孤立波解で下のようなものである．

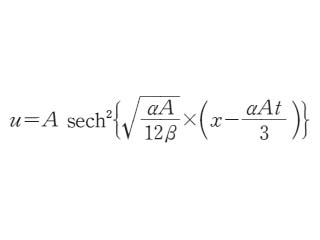
ここで A は孤立波の高さに相当する定数である．

出典　朝倉書店