一次変換（読み）イチジヘンカン（英語表記）linear transformation

デジタル大辞泉

いちじ‐へんかん〔‐ヘンクワン〕【一次変換】

平面上の点から平面上の点への写像。点（x,y）と点（x′,y′）の関係が一般にx′＝ax＋by, y′＝cx＋dyという一次式で表されるもの。線形変換。線型写像。

出典　小学館

精選版 日本国語大辞典

いちじ‐へんかん ‥ヘンクヮン【一次変換】

〘名〙

① ベクトル空間からベクトル空間へのある種の写像。ベクトル空間Ｕからベクトル空間Ｖへの写像ｆのうち、f(αa+βb)=αf(a)+βf(b) （ａ、ｂはＵの要素、α、βは実数）をみたすものをＵからＶへの一次変換という。

② 複素数に複素数を対応させるある種の写像。z′=(az+b)/(cz+d) という形で表わされるようなもの。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

一次変換 (いちじへんかん)
linear transformation

直線，平面，空間のように座標が定まっているものの間の写像で，座標について一次式で表されるものを一次変換という。例えば座標X，Y，Zが定まった空間の間の写像fで，点（x，y，z）をf（x，y，z）＝（a₁x＋b₁y＋c₁z，a₂x＋b₂y＋c₂z，a₃x＋b₃y＋c₃z）に移すものは一次変換である。この考えは，一般のn次元線形空間Vからm次元線形空間Wへの写像fに拡張される。x₁，……，x_nをVの基底，y₁，……，y_mをWの基底とする。Vの元xを（α_j：スカラー）と書けば，となり，このときfは一次変換といわれる。各f（x_j）はWの元であるから，（α_ij：スカラー）と書ける。一次変換の性質から，となり，fは（m，n）行列で完全にきまる。Vの元を列ベクトルで表示すれば，変換f（x）は行列の積で表せる。一次変換は無限次元空間でも同じように考えられる。一次変換は線形空間の間の線形写像と実質的に同じであり，一次変換という言葉で線形写像を意味することもある。また，一次分数変換のことを単に一次変換ということもある。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

一次変換
いちじへんかん

行列を与えたとき、それによって定まる空間から空間への写像のこと。A＝(a_ij)をm行n列の行列とする。n次元空間E_n内の点P(x₁，……，x_n)に対して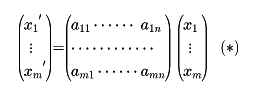

によって点P′(x₁′，……，x_m′)が定まる。点P′はm次元空間E_mの点である。m行n列の行列Aに対して、このようにして定まるE_nからE_m内への写像を、Aで定まる一次変換という。たとえば、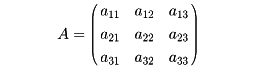

のとき、空間の点P(x₁，x₂，x₃)に対して（＊）を成分ごとに書くと次のようになる。

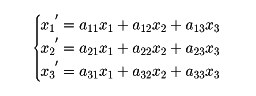
空間の点（x₁，x₂，x₃）に、この式によって、空間の点（x₁′，x₂′，x₃′）が定まる。

　一次変換は、直線を直線または点に、平面を平面か直線か点に写像する、という性質をもっている。またn次元ベクトル
　　x＝(x₁，……，x_n)
に対して、（＊）で定まるm次元ベクトル
　　x′＝(x₁，……，x_m)
を対応させる。この写像をn次元ベクトル空間V_nからm次元ベクトル空間V_mへの一次変換という。この写像fは、ベクトルの演算について次の性質をもつ。

　　f(k₁x₁＋k₂x₂)＝k₁f(x₁)＋k₂f(x₂)
これを一次変換fの線形性という。

［寺田文行］

[参照項目] | 行列 | 線形性

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の一次変換の言及

【座標】より

…簡単な例として，は，原点をxy平面内で点(a,b)に平行移動し，さらにその点のまわりに角度αの回転を行った直交座標系(x′，y′，z′)によってもとの(x,y,z)を表す場合である。一般に旧座標系｛x_i｝が新座標系｛x_i′｝の一次式の場合，すなわち(1)が具体的に，で与えられるような座標変換は一次変換と呼ばれ，行列の記法を用いてx＝Ax′＋aで示すことができる。ここでA＝(a_ij)はa_ijを要素とするn行n列の行列，a＝(a_i)はn次の列ベクトル(n行1列行列)である。…

※「一次変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」