関係（読み）カンケイ

デジタル大辞泉

かん‐けい〔クワン‐〕【関係】

［名］(スル)
１ 二つ以上の物事が互いにかかわり合うこと。また、そのかかわり合い。「前後の関係から判断する」「事件に関係する」
２ あるものが他に対して影響力をもっていること。また、その影響。「気圧の関係で耳鳴りがする」「国の将来に関係する問題」
３ 人と人との間柄。また、縁故。「あの人とはどういう関係ですか」「友好関係を結ぶ」「父親の関係で入社する」
４ 性的に交わること。「人妻と関係をもつ」「妻子のある男性と関係する」
５ （他の名詞の下に付いて）その方面。そういう領域。「音楽関係の仕事」「アウトドア関係の雑誌」
[類語]（1）関連・連関・連係・相関・関与・交渉・係かかわり・繋つながり・結び付き・掛かり合い・引っ掛かり・絡み・掛かりっきり（―する）関する・係かかわる・係かかる・まつわる・係かかずらう・与あずかる・絡む・掛かり合う・関わり合う・巡る・かまける／（3）間柄・間あいだ・仲・続き合い・続き柄・縁えん・えにし・ゆかり・縁故えんこ・誼よしみ・恋仲／（4）性交・交合・情交・セックス・ファック・エッチ・交接・交尾・性行為・房事・同衾・共寝・夜伽・性交渉・性生活・夫婦生活・合歓・一儀・寝る・抱く・枕を交かわす・夜の営み

出典　小学館

精選版 日本国語大辞典

かん‐けいクヮン‥【関係・関繋・管係】

1. 〘 名詞 〙 二つ以上の物事が互いにかかわりあうこと。また、そのかかわりあい。
2. ① ( ━する ) ある物事が、他の物事に影響すること。また、その影響。
   1. [初出の実例]「天下の大事に関係した者は」(出典：史記抄（1477）一五)
   2. 「職業の貴賤は、人品の高下に関係せざる事を知るべし」(出典：西国立志編（1870‐71）〈中村正直訳〉九)
   3. [その他の文献]〔鶴林玉露‐一五〕
3. ② ( ━する ) ある物事が、他の物事につながりを持つこと。また、そのつながり。
   1. [初出の実例]「此事於_二吾道_一関係尤為_レ大焉」(出典：藤樹文集（1648頃）四)
   2. 「イヤイヤどうでも医業に関係(クヮンケイ)しておっては」(出典：安愚楽鍋（1871‐72）〈仮名垣魯文〉三)
4. ③ 人と人との間柄。かかわりあい。
   1. [初出の実例]「しかし君と我輩とは親友の関繋(クヮンケイ)ぢゃ無いか」(出典：浮雲（1887‐89）〈二葉亭四迷〉二)
5. ④ ( ━する ) 男女が肉体的な交わりをすること。情交。
   1. [初出の実例]「笹村はそも何時(いつ)頃から夫人と関係して居たのであらうか」(出典：地獄の花（1902）〈永井荷風〉一四)
6. ⑤ ( 多く名詞の下に付けて ) その方面。そういう分野。「教育関係の仕事」「繊維関係の会社」
7. ⑥ 集合Ａ、Ｂの直積 A×B の部分集合のＡ、Ｂに対する称。すなわち、A×B の部分集合Ｒを、Ａの元とＢの元との関係という。A×B の元（a, b）は、Ｒに属するとき、関係Ｒにあるといわれる。ＡとＢとが等しいときは、Ａの上の関係ということがある。

関係の語誌

( 1 )中国、宋代以降の口語語彙と思われる。
( 2 )中世以降、日本でも「史記抄」などの抄物では中国の用法に沿う①の意の例が見られる。しかし、幕末に、蘭学系統の人たちが②の意味に用いはじめ、その後、「哲学字彙」を経て定着した。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

関係 (かんけい)
relation

哲学用語。伝統的なヨーロッパの存在観においては，独立自存する〈実体〉なるものがまずあって，実体どうしの間に，第二次的に〈関係〉が成立するものと考えられてきた。これに対して，〈関係〉こそが第一次的な存在であり，いわゆる実体は〈関係の結節〉ともいうべきものにすぎないと考える立場が，仏教の縁起観など，古くから存在したが，現代においてはこの〈関係主義〉的存在観が優勢になりつつある。ところで，〈関係〉とは何であり，それにはいかなる種類があるかについての分析的討究は，仏教哲学においても，西洋哲学においてもロックやD.ヒューム以来おこなわれているが，スタンダードな総括的定見はまだ確立していない。論理学や数学基礎論，社会諸科学などにおける〈関係〉の規定や分類も，現状ではまだ周到とは言えない。暫定的には〈一者－他者〉的に分節可能な両契機の間に，一者が当の一者としてあるのは当該他者に〈対して〉であり，他者が当の他者としてあるのは当該一者に〈対して〉であるごとき態勢が存立するとき，この〈一者－対－他者〉を存在的関係と定義する。一者が当の一者としてあるのは当該他者に〈因（よ）って〉であるときを機能的関係と呼び，一者が当の一者としてあるのは当該他者に〈拠（よ）りて〉であるときを論理的関係と呼ぶ。関係を〈関係〉として定義する真の要件は〈として〉〈ある〉および，上に言う〈対して〉〈因って〉〈拠りて〉を存在論的・認識論的に規定することにかかっている。なお，関係の分類は，関係を一種の〈もの〉として〈類－種〉的に分類したのでは不可であり，関係をあくまで〈こと〉として弁証法的に定位する〈上向法〉にまたねばならない。
→弁証法
執筆者：廣松 渉

関係 (かんけい)
relation

数学用語。集合Xと集合Y（X＝Yでもよい）の元x，yに関する命題で，x，yを定めれば真偽が確定するとき，その命題を関係または2項関係という。X＝Y＝（実数全体）のときの〈x≧y〉，Y＝（Xの部分集合全体）のときの〈x∈y〉などはその例である。一つの関係をRで表したとき，x，yについてその命題が真であるとき，x，yはその関係を満たすといい，xRyと書く。x≧y，x∈yなどの≧，∈は上のRの例である。一つの関係Rに対して，yR⁻¹x⇔xRyによって定まる関係R⁻¹をRの逆関係という。≧の逆関係は≦である。X＝Yのとき，（1）すべてのx∈XについてxRxであれば，Rは反射的，（2）RとR⁻¹とが同じであれば，Rは対称的，（3）xRyかつyRzならばxRzが成り立つならば，Rは推移的，（4）xRyかつyRxならばx＝yであるならば，Rは反対称的であるという。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

関係
かんけい
relation 英語
Beziehung ドイツ語
rapport フランス語

論理学では、かなり形式的に、関係を分類する。たとえば、「Rがaとbとの間に成り立てば、bとaとの間にも成り立つ」という条件を満たす関係Rは「可逆的な関係」とよばれ、「Rがaとbとの間に成り立ち、またbとcとの間にも成り立てば、aとcとの間にも成り立つ」という条件を満たす関係Rは「推移的な関係」とよばれる。一例をあげれば、友人関係は、一般に可逆的な関係であるが、推移的な関係ではない。なお、論理学では、普通の関係のほか、3項関係、4項関係など、一般にn項関係も考える。

　たとえば2項関係の場合、その関係の成立する対の全体からなる集合を使ってこの関係を代表させることができる。こうして一般に関係を集合とみなすことにより、集合論の成果を関係についての議論に適用することができるようになり、その結果「関係の論理学」が見通しのよいものとなった。

［吉田夏彦］

[参照項目] | 集合論

出典　小学館　日本大百科全書(ニッポニカ)

普及版 字通

【関係】かん（くわん）けい

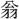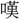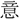
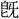かかわり。〔甌北詩話、六〕放（陸游）は則ち轉じて、詩外の事を以て盡(ことごと)く詩中に入る。～或いは大聲疾呼、或いは長言永す。命に關係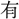り、出語自(おのづか)ら沈雄なるを覺ゆ。

字通「関」の項目を見る。

出典　平凡社「普及版 字通」

ブリタニカ国際大百科事典 小項目事典

関係
かんけい
relation

集合の2要素の間の特別な性質。現在の数学で，関係を表現するには集合を利用する。集合 A の元 x∈A と，集合 B の元 y∈B とが，ある関係 R を満たすかどうかが確定しているということは，この関係を満たすような (x，y) の集合
{(x，y)｜xRy}⊂A×B
を指定することで得られる。そのため A×B の部分集合自体を，A と B の元の間の関係という。たとえば，実数について，{(x，y)｜x≦y} という半平面で順序 ≦ が，対角線 {(x，y)｜x＝y} で相等 ＝ が規定できる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

関係(哲学)【かんけい】

哲学，論理学用語。最広義には事象や概念の結びつき方。類似や対立，因果など。アリストテレスはカテゴリーを10個とし，その一つとして関係をあげた。またカントは実体と属性，原因と結果および相互作用を関係のカテゴリーとした。伝統的に，独立自存する実体がまずあり，その実体のあいだに〈関係〉が成立すると考えられてきたが，むしろ関係こそが第１次的であるとする存在論が近年の動向。

出典　株式会社平凡社

デジタル大辞泉プラス

関係

後藤明生(めいせい)の短編小説。1962年、第1回文藝賞中・短編部門佳作受賞。

出典　小学館

ASCII.jpデジタル用語辞典

関係

「リレーションシップ」のページをご覧ください。

出典　ASCII.jpデジタル用語辞典

世界大百科事典（旧版）内の関係の言及

【関係】より

…数学用語。集合Xと集合Y(X＝Yでもよい)の元x,yに関する命題で，x,yを定めれば真偽が確定するとき，その命題を関係または2項関係という。X＝Y＝(実数全体)のときの〈x≧y〉，Y＝(Xの部分集合全体)のときの〈x∈y〉などはその例である。一つの関係をRで表したとき，x,yについてその命題が真であるとき，x,yはその関係を満たすといい，xRyと書く。x≧y,x∈yなどの≧，∈は上のRの例である。一つの関係Rに対して，yR^－1x⇔xRyによって定まる関係R^－1をRの逆関係という。…

※「関係」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」