線形性（読み）せんけいせい（その他表記）linearity

日本大百科全書(ニッポニカ)

線形性
せんけいせい
linearity

二つの原因A、Bが共存するとき、その結果が、Aの結果とBの結果の和となるなら、この原因と結果の関係は線形であるという。正確にいえば、任意の数x₁、……、x_n、y₁、……、y_nとtに対し、
(1)f(x₁＋y₁,……,x_n＋y_n)
　　 ＝f(x₁,……,x_n)
　　 ＋f(y₁,……,y_n)
(2)f(tx₁,……,tx_n)
　　 ＝t・f(x₁,……,x_n)
の二つの性質をもつ関数fは線形である。あるいはfは線形性をもつという。変数X₁、……、X_nの同次一次式
　　f(X₁,……,X_n)＝a₁X₁＋……＋a_nX_n
は線形性をもつ。平面上の直線が、この直線上に原点をもつ(x,y)座標で、二つの変数xとyの同次一次式で表されることからこの名が生まれた。線形性に関する数学理論をまとめたものが線形代数である。その基本概念である線形空間と線形写像は、線形性をはっきりさせる立場で述べると、次のようになる。

　n次元線形空間Vとは、Vの基底とよばれるn個の元e₁、……、e_nの形式的一次式
　　x₁e₁＋……＋x_ne_n （x_iは数）
で表される元全体の集合で、Vの元の和とVの元の定数倍を、それぞれ、
(3)(x₁e₁＋……＋x_ne_n)
　　 ＋(y₁e₁＋……＋y_ne_n)
　　 ＝(x₁＋y₁)e₁＋……
　　 ＋(x_n＋y_n)e_n
(4)t(x₁e₁＋……＋x_ne_n)
　　 ＝(tx₁)e₁＋……＋(tx_n)e_n
で定義したものをいう。ここで、x_i、y_i、tは数である。さらに、線形空間Vから線形空間Wへの写像Tが、Vの元x、yと数tに対し
(5)T(x＋y)＝T(x)＋T(y)
(6)T(tx)＝tT(x)
を満たすとき、TをVからWへの線形写像という。(1)、(3)、(5)は同じ種類の式であり、(2)、(4)、(6)もそうであることは容易にわかる。

　今日、数学や物理学などで広く「線形」ということばが用いられているが、そのいずれの場合も、線形空間と線形写像の考え方によって、そう名づけられている。たとえば、
(7)

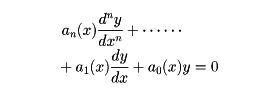
を線形常微分方程式というのは、xの関数yを(7)の左辺D(y)に写す写像Dが、n回微分可能な関数の線形空間から関数の線形空間への線形写像になっていることによる。

［菅野恒雄］

　線形性のもっとも簡単な例としては、ばねの伸びXと、それだけ伸ばしたときの引き戻しの力Yとの関係がある。XとYとの間には、フックの法則
　　Y＝kX　（kはばね定数）
が成り立ち、これは線形性を満たす。しかしこの関係は、伸びXがある限界（弾性の限界）を超すと破れてしまう。Xが小さい間も線形性は実は近似的なものである。実際に、もし関係式Y＝F(X)がX＝0の近傍で少なくとも1回微分可能であり、さらにF(0)＝0ならば
　　Y＝F'(0)X＋o(X)　(X→0)
となり、Xが十分に小さい間は、XとYは線形関係にあるとみなすことができる。ただし、o(X)は、X^1＋α(α＞0)に比例する量を表す。この意味で、単振動の線形方程式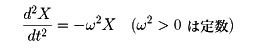

も非常に多くの場合に成り立つ。この場合、加速度d²X/dt²をYと考える。この方程式をX＝x₁(t)が満たしX＝x₂(t)が満たすなら、任意の定数λ、μによる重ね合せ
　　X(t)＝λx₁(t)＋μx₂(t)
も満たす。これを線形な方程式の定義としてもよい。振動の運動方程式は、振幅が大きくなると一般に非線形になる。しかし、物理学の基本法則には厳密に線形と信じられているものも多い。電磁気学のマクスウェルの方程式も、量子力学のシュレーディンガー方程式、ディラック方程式も、いずれも線形である。ニュートンの運動の第二法則も力と加速度の間の線形な関係であるが、光速に近い運動に対しては質量が速度に依存してきて線形性が破れる。

［江沢　洋］

[参照項目] | 重ね合せの原理

出典　小学館　日本大百科全書(ニッポニカ)