二項級数（読み）にこうきゅうすう（英語表記）binomial series

改訂新版　世界大百科事典

二項級数 (にこうきゅうすう)
binomial series

実数α≠0と整数n≧0に対して，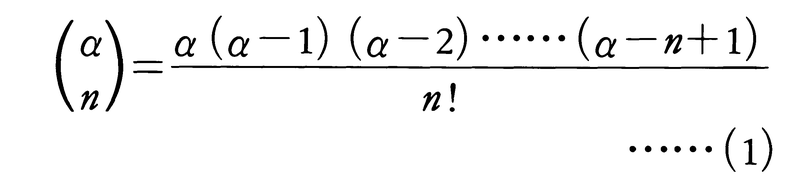

と定義する（αがn以上の自然数Nのときは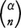は組合せの数_nC_nである）。このとき関数f（x）＝（1＋x）^αのx＝0を中心とするテーラー展開は次のようになる。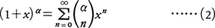

ただし，右辺の級数は一般には－1＜x＜1で収束し，α＞0ならば－1≦x≦1で収束，－1＜α＜0ならば－1＜x≦1で収束する。とくにαが自然数ならば，（2）の右辺でn＞αなる項は0になることが（1）からわかるから，（2）はすべての実数xで成立し，これはふつうの二項定理である。一般のαに対する（2）の右辺の級数を二項級数といい，（1）を一般化された二項係数という。（2）のxを複素数zで置き換えた級数も二項級数といい，この級数の収束半径は1である。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

二項級数
にこうきゅうすう

「二項定理」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典