級数（読み）キュウスウ（その他表記）series

デジタル大辞泉

きゅう‐すう〔キフ‐〕【級数】

１ 数学で、数列の各項を順に加法記号（＋）で結んだもの。例えば、数列［a_n］で、a₁＋a₂＋a₃＋…＋a_n＋…をいう。項が有限個であれば有限級数、無限個であれば無限級数という。
２ 写真植字の文字の大きさを級で表す数。最小7級から最大100級まで24種あり、1級は4分の1ミリ、13級がほぼ9ポイントにあたる。

出典　小学館

精選版 日本国語大辞典

きゅう‐すうキフ‥【級数】

1. 〘 名詞 〙
2. ① 数列の項を加法記号で順次に結合して得られる式。数列の項が有限のとき有限級数、無限のとき無限級数という。以前は、数列の意味にも用いた。〔工学字彙（1886）〕
3. ② 「むげんきゅうすう（無限級数）」の略。
4. ③ 階段の段数。
   1. [初出の実例]「女坂は一百七級ありて、級数多かれども、一級毎に広狭を交々にし」(出典：東京風俗志（1899‐1902）〈平出鏗二郎〉上)
5. ④ 写真植字の文字の大きさを表わす単位「級」の度合。〔実用印刷技術（1957）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

級数 (きゅうすう)
series

ある規則に従って順次に並べられた数または関数の列を，それぞれ数列または関数列といい，それらの列を順次に加法記号で結合した式を級数という。例えば｛1，3，5，7，……｝，｛1，2，4，8，……｝は数列であり，これらに対応する級数は，それぞれ1＋3＋5＋7＋……，1＋2＋4＋8＋……である。数列，関数列または級数を構成する各要素を，その数列，関数列または級数の項という。上の第1の例のように各項とその次の項との差が一定である級数を等差級数arithmetic seriesまたは算術級数といい，第2の例のように各項とその次の項との比が一定である級数を等比級数geometric seriesまたは幾何級数という。また，等差級数の各項の逆数を項とする級数を調和級数harmonic seriesという。項数が有限である級数を有限級数といい，項数が無限にある級数を無限級数ということがあるが，単に級数といえば，ふつうは無限級数を意味する。

　第n項がa_nである無限級数a₁＋a₂＋……＋a_n＋……を形式的にで表す。その第n項までの和を第n部分和，または単に部分和という。s_nが簡単な式で表される級数の例として，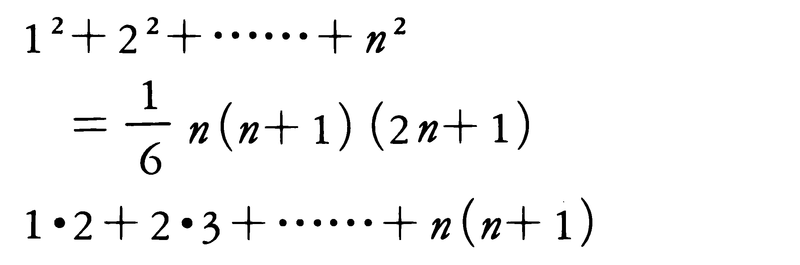



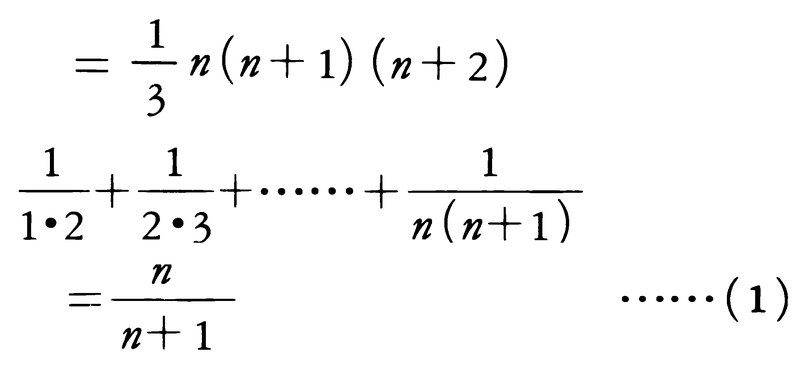
などがある。また〈等差数列〉　〈等比数列〉の項目にも述べられているように，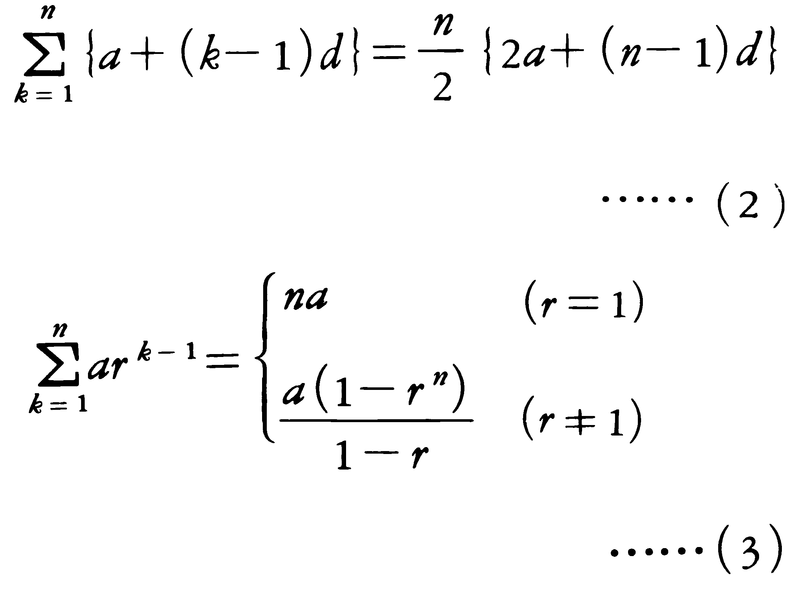

　与えられた級数の部分和の数列｛s_n｝において，nが限りなく大きくなるときs_nがある定まった値sに限りなく近づくならば，すなわち数列｛s_n｝が極限値sをもつならば，その級数は収束して和sをもつ，またはsに収束するといい，このことを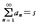

と書く。それ以外の場合には級数は発散するという。例えば，（1）からわかるように，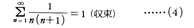

であるが，は発散する。また（3）からわかるように等比級数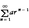は｜r｜＜1ならば\(\frac{a}{（1－r）}\)に収束し，｜r｜≧1ならば発散する。

　収束する級数において，各項の絶対値をとって作った級数も収束するとき，もとの級数は絶対収束であるといい，そうでないとき，条件収束であるという。例えば上記（4）の級数や，｜r｜＜1のときの等比級数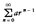は絶対収束である。また，級数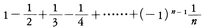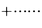は収束し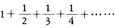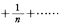，は発散することが知られていることから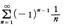，は条件収束である。

　各項が負でない実数から成る級数を正項級数という。正項級数の部分和の列は単調増加であるから，正項級数が収束することと，その部分和の列が有界なこととは同等である。正項級数は，その項の順序をどのように入れかえても，その収束・発散は変わらないし，収束する場合はその和も変わらない。正項級数については多くの収束判定法が知られているが，いくつかの例をあげる。Σa_nが正項級数で数列｛a_n｝が単調減少のとき，（1）Σa_nは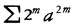と同時に収束または発散する。（2）［1，∞）で定義された，単調減少関数f（χ）でf（n）＝a_nなるものが存在すれば，Σa_nと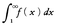とは同時に収束または発散する。例えばΣ1/n^αはα≦1ならば発散，α＞1ならば収束する。また，Σa_n，Σb_nを正項級数とするとき，正の定数kがあって有限個のnを除きa_n≦kb_nが成立するならば，Σb_nが収束するときΣa_nも収束し，Σa_nが発散するときΣb_nも発散する。

　関数項の級数では，変数の値により収束・発散の事情が変わる。級数が収束するような変数の値の範囲をその級数の収束域という。関数項の級数は，その収束域では和の関数を定義する。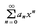（a_nは定数）の形の級数はべき級数と呼ばれ，関数項の級数の代表的なものである。これについて

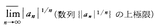の逆数をRとすると，この級数の収束域は｜x｜＜Rなるxの全体，またはそれにx＝R，－Rの一方あるいは両方をつけ加えた範囲である。例えば級数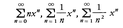に対して，上記のRはいずれも1であるが，収束域はそれぞれ｜x｜＜1，－1≦x＜1，－1≦x≦1なるxの全体である。べき級数は微分積分学や関数論において，関数を表示する主要な役割を演じ，応用上も関数値の近似計算の手段として広く用いられる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

級数
きゅうすう
series

数列a₁, a₂,……, a_n,……があるとき、これをプラスで結んだa₁＋a₂＋……を級数という。これを記号で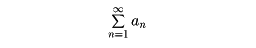

と表す。これは、数列a₁, a₂,……を順に足していくとどうなるか、ということが問題とされるということである。いま、
　　s_n＝a₁＋a₂＋……＋a_n
として、これを級数a₁＋a₂＋……の部分和という。この部分和のつくる数列s₁, s₂,……がある値sに収束するとき、級数a₁＋a₂＋……は収束して、その和はsであるといい、これを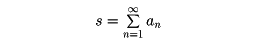

で表す。そうでないときは、級数は発散するという。とくにs_nが正の無限大に発散するとき、級数は正の無限大に発散するという。級数の各項が正の数（非負の数）であるとき、この級数を正項級数という。また、級数の各項の絶対値をとってつくった級数が収束するとき、この級数は絶対収束であるという。ディリクレおよびリーマンは、級数が収束ではあるが絶対収束ではないときは、項の順序を適当に変更すれば、任意の値に収束させたり、あるいは発散させたりできることを示した。

　級数についての次の二つの性質は、解析学のバックボーンとなる重要な定理である。

〔1〕正項級数は、収束するか、または正の無限大に発散する。そしてその状態、あるいは収束したときの和は、級数の項の順序を入れ替えたり、あるいは項をくくり直したりしても影響がない。

〔2〕絶対収束級数は収束する。そして、その和は、級数の順序を入れ替えたり、あるいは項をくくり直したりしても影響がない。

　いろいろな級数が古くから考察され、その和を求める方法もいろいろくふうされた。いろいろな値を求めるとき、級数を利用することが多い。しかし、特別な場合を除いて、部分和の表示をつくり、それがどうなっていくかを見定めることは困難である。そこで、級数が収束するか発散するかを判定する方法がいろいろ考案された。次はその一つである。二つの正項級数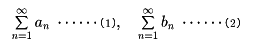

があって、その項の間に、a_n≦b_n (n＝1, 2,……)という関係が成り立っているとする。このとき、(2)が収束するならば(1)も収束する。また、(1)が発散するならば(2)も発散する。

　級数の項の符号が交互にプラス、マイナスを繰り返すとき、交項級数または交代級数という。交項級数に関する次の定理は、実用的な意味をもっている。

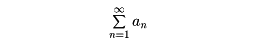
が交項級数で、|a₁|≧|a₂|≧……、かつ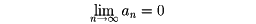

ならば、この級数は収束する。そして、その和をsとするとき、部分和s_nについて、
　　|s_n－s|≦|a_n+1|
が成り立つ。

　級数の積をつくったりする必要もおこる。

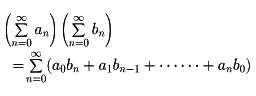
というような計算ができるとよいが、たとえば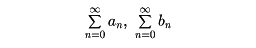

がともに収束で、とくにその一方が絶対収束ならば、このことは成り立つ。

　級数が発散するときも、これに適当な方法である値を付与し、これを利用することを考えることがある。たとえば、チェザロの総和法は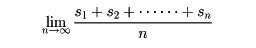

とする。アーベルの総和法は、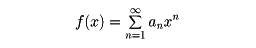

として、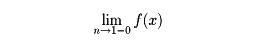

を求める。これによれば、発散する級数
　　1－1＋1－1＋……
には、どちらの方法によっても、1/2という値が付与される。

［竹之内脩］

[参照項目] | 一様収束 | 整級数 | フーリエ級数

いろいろな級数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

級数
きゅうすう
series

数列 a₁，a₂，…，a_n，… の項を順に和の記号 ＋ で結んで得られる式 a₁＋a₂＋…＋a_n＋… をいう。 a₁，a₂，…，a_n，… を級数の項，a_n をその第 n 項という。項の数が無限個あるときは無限級数といい，有限個の場合は有限級数と呼ぶ。無限級数は直和記号 Σ を用いて次のように表わす。
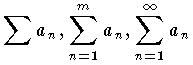有限級数は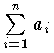， で表わす。有限級数において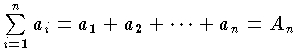， とするとき，この A_n を級数の和という。無限級数 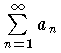に対しては A₁＝a₁，A_n＝A_n-1＋a_n＝a₁＋a₂＋…＋a_n-1＋a_n(n≧2) によって定義される A_n を第 n 項までの部分和という。数列 {A_n} は極限値をもつこともあり，もたないこともあるが，もし {A_n} が収束して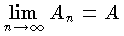， が存在すれば，この A を級数の和と呼ぶ。ただし，A は有限でも無限でもよい。この和が有限のとき，無限級数 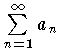は収束するといい，収束しない場合を発散するという。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

級数【きゅうすう】

一定の規則に従って並んだ数または関数（数列または関数列）の各項を和の記号で結んだもの。一般の形はa₁＋a₂＋…＋a(/n)＋…。項の数が有限なら有限級数，無限なら無限級数という（収束，発散）。等差級数，等比級数，べき級数，フーリエ級数等種々ある。
→関連項目調和級数

出典　株式会社平凡社

普及版 字通

【級数】きゆうすう

階級の上下の数。

字通「級」の項目を見る。

出典　平凡社「普及版 字通」