精選版 日本国語大辞典 「二項定理」の意味・読み・例文・類語
日本大百科全書(ニッポニカ) 「二項定理」の意味・わかりやすい解説
二項定理
にこうていり
二項の代数和のn乗(nは正整数)の展開公式を二項定理という。式で書けば、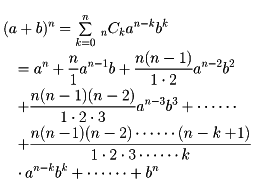
となる。各係数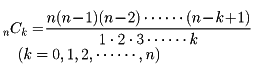
を二項係数といい、これをまた記号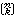 で表すこともある。このnCkの数値はn個の異なるものからk個のものを選び出す仕方(選出の順序は考えない)の総数である(組合せの数)。二項定理は組合せ理論と関係し、二項係数についての性質はパスカルによって明らかにされた。そのなかの有名なものにパスカルの三角形がある。これは二項係数間の関係
で表すこともある。このnCkの数値はn個の異なるものからk個のものを選び出す仕方(選出の順序は考えない)の総数である(組合せの数)。二項定理は組合せ理論と関係し、二項係数についての性質はパスカルによって明らかにされた。そのなかの有名なものにパスカルの三角形がある。これは二項係数間の関係
nCk-1+nCk=n+1Ck (1≦k≦n)
を三角形状に数を並べて示したものである。
二項定理における正整数のべき指数nを一般の実数αで置き換えた展開公式を一般二項定理という。この場合、展開項の個数は無限となる。たとえば、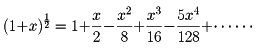
となる。右辺をxの二項級数という。この級数が和をもつ(収束する)ためのxのとりうる値の範囲(収束域)は-1≦x≦1である。
一般に(1+x)αを二項級数に展開したとき、その収束域はα>0ならば-1≦x≦1となり、また、-1<α<0ならば-1<x≦1となる。α=0またはαが自然数ならばxはどんな数でも収束する。一般二項級数はI・ニュートンによって研究された。
[竹内芳男]
改訂新版 世界大百科事典 「二項定理」の意味・わかりやすい解説
二項定理 (にこうていり)
binomial theorem
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「二項定理」の意味・わかりやすい解説
二項定理
にこうていり
binomial theorem
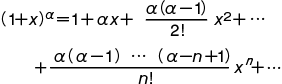 ここに n!=1・2・3・…・n で,n の階乗と読む。上の展開式における右辺の級数を二項級数またはニュートン級数といい,その係数 {α(α-1)…(α-n+1)}/n! を二項係数という。これを
ここに n!=1・2・3・…・n で,n の階乗と読む。上の展開式における右辺の級数を二項級数またはニュートン級数といい,その係数 {α(α-1)…(α-n+1)}/n! を二項係数という。これを 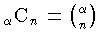 と書くことがある。たとえば α=1/2 の場合は,-1≦x≦1 のとき,
と書くことがある。たとえば α=1/2 の場合は,-1≦x≦1 のとき,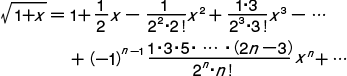 である。αが自然数ならば,二項係数は α≧n のときα個から n 個とってできる組合せの個数を表わす。 αCn ,α<n のとき0であるから,(1+x)α=1+αC1x+αC2x2+…+αCnxα となる。これが古くから知られている二項定理である。
である。αが自然数ならば,二項係数は α≧n のときα個から n 個とってできる組合せの個数を表わす。 αCn ,α<n のとき0であるから,(1+x)α=1+αC1x+αC2x2+…+αCnxα となる。これが古くから知られている二項定理である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「二項定理」の意味・わかりやすい解説
二項定理【にこうていり】
→関連項目多項定理
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の二項定理の言及
【多項定理】より
…ただし,![]() による和は,nを負でない整数p1,……,pnの和n=p1+p2+……+pkに分解するすべての場合にわたるものとする。k=2のとき二項定理という。多項定理の応用例を二つあげる。…
による和は,nを負でない整数p1,……,pnの和n=p1+p2+……+pkに分解するすべての場合にわたるものとする。k=2のとき二項定理という。多項定理の応用例を二つあげる。…
※「二項定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

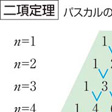

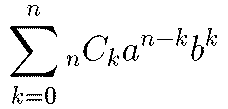 (ただし、nCk=n!/((n-k)!k!))が成り立つというもの。
(ただし、nCk=n!/((n-k)!k!))が成り立つというもの。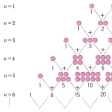
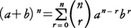 で与えられる。ただし, ここで係数
で与えられる。ただし, ここで係数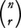 は二項係数と呼ばれ,
は二項係数と呼ばれ, である。これを二項定理という。1≦r≦nに対して,
である。これを二項定理という。1≦r≦nに対して,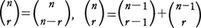 これより,(a+b)n⁻1の展開における第r項と第r+1項との係数の和は,(a+b)nの展開における第r+1項の係数に等しいことがわかる。これら二項係数を順々に並べて書いた
これより,(a+b)n⁻1の展開における第r項と第r+1項との係数の和は,(a+b)nの展開における第r+1項の係数に等しいことがわかる。これら二項係数を順々に並べて書いた