余因子（読み）よいんし

日本大百科全書(ニッポニカ)

余因子
よいんし

n次の正方行列Aにおいて、その第i行および第j列を除いてできる(n-1)次の正方行列の行列式をD_ijとする。すなわち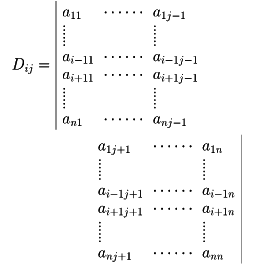

D_ijを行列Aの（i,j）成分a_ijの小行列式という。D_ijに
　　A_ij=(-1)^i+jD_ij
のようにして符号をつけた数を(i,j)成分a_ijの余因子、または余因数という。余因子の一つの役割は、行列式の余因子展開である。行列Aのi行の成分の余因子を
　　A_i1,A_i2,……,A_in
とすると、Aの行列式detAを次のように表すことができる。

（1）detA=a_i1A_i1+a_i2A_i2+……+a_inA_in
同様に第j列の成分の余因子によって
（2）detA=a_1jA_1j+a_2jA_2j+……+a_njA_nj
と表すことができる。（1）、（2）を行列式の余因子展開という。

　余因子の第二の役割は、行列Aの逆行列A^-1への応用である。すなわちdetA≠0のとき、Aの逆行列は次のように表される。

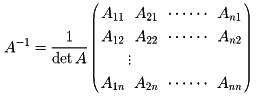
この右辺に書かれた行列は余因子の行列(A_ij)の転置行列である。

［寺田文行］

[参照項目] | 行列 | 行列式

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の余因子の言及

【行列式】より

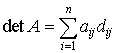…したがって，例えば，　det(a₁＋c₂a₂＋……＋c_na_n,a₂，……，a_n)　　＝det(a₁,a₂，……，a_n)(7)n次正方行列Aに対して，そのi行およびj列を除いてできるn－1次の行列A_ijをとる。(－1)^i＋jdetA_ij＝d_ijとおくと，　各j＝1,2，……，nについて　各i＝1,2，……，nについて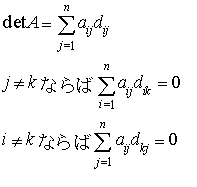上で得た値d_ijをAの(i,j)余因子という。d_ijを(i,j)成分にもつ行列D＝(d_ij)を考えれば，上の関係はA(^tD)＝(^tD)A＝(det A)I(Iはn次の単位行列)ということと同じである。…

【小行列式】より

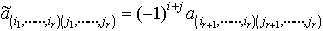…Aがn次の正方行列の場合，｛1，……，n｝から｛i₁，……，i_r｝を除いた自然数の小さい順に並べたものを(i_r＋1，……，i_n)と書くことにし，i₁＋……＋i_r＝i,j₁＋……＋j_r＝jとして，とおく。これは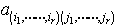の余因子といわれる。(i₁，……，i_r)，(j₁，……，j_r)を固定すると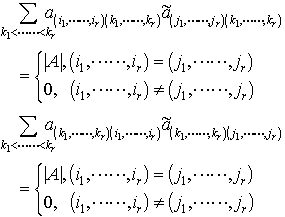，これは行列式のある行または列についての展開の一般化になっており，ラプラスの展開定理といわれる。…

※「余因子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」