点集合論（読み）てんしゅうごうろん

日本大百科全書(ニッポニカ)

点集合論
てんしゅうごうろん

ある与えられた空間の点を要素とする集合を点集合といい、点集合の位相的性質を調べることを点集合論という。n次元ユークリッド空間Eⁿを考える。Eⁿの点xと正の実数εに対し、xとの距離がεより小さいEⁿの点の集合をxのε近傍という。AをEⁿの点集合とする。Eⁿの点xのどのようなε近傍もx以外のAの点を含むとき、xをAの集積点という。Aの点とAの集積点の全体をAの閉包という。Aがその閉包に等しいときAを閉集合という。Aのどの点に対してもその適当なε近傍がAに含まれるとき、Aを開集合という。さらに適当な球にAが含まれるときAは有界であるという。次の一連の定理は点集合論においてとくに重要である。Eⁿの有界な無限集合はかならず集積点をもつ（ボルツァノ‐ワイアシュトラースの定理）。Eⁿの有界閉集合の列F_kがF_k⊃F_k+1,k=1,2,…を満たすならば、そのすべての交わりは空でない（カントルの共通部分定理）。FをEⁿの有界閉集合、G_λ,λ∈ΛをRⁿの開集合の族で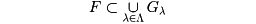

であるものとする。このときこのG_λから適当な有限個のG_λ1,G_λ2,‥‥,G_λmを選べば、すでに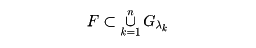

である（ハイネ‐ボレルの定理）。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の点集合論の言及

【集合論】より

…連続体仮説(または一般連続体仮説)を公理として採用したとき，通常の公理系とは独立であることが証明されている，ということは，集合の構成を制限することによって一般連続体仮説の成り立つような集合の体系を作ることもでき，また，反対に，実数全体の集合の部分集合を適当にとれば，濃度が可算無限より大きく，実数の濃度より小さいものがとれる(が，それはふつうの構成法ではできない)ことを示している。
［点集合論］
　ある次元のユークリッド空間Eの部分集合は，Eの点を元としているので点集合と呼ばれる。点集合についての理論を点集合論と呼び，これが集合論の主要部分と考えられた時代もあるが，その内容の大部分は，現在では〈位相空間の部分集合〉として一般化された立場で扱われるようになった。…

※「点集合論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」