無限積（読み）むげんせき（英語表記）infinite product

改訂新版　世界大百科事典

無限積 (むげんせき)
infinite product

無限乗積ともいう。｛a_n｝を与えられた数列とし，いずれも0でないとする。形式的な積a₁a₂a₃……を無限積といい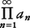，またはПa_nと書く。最初のn項の積p_n＝a₁a₂……a_nを第n部分積という。数列｛p_n｝が0でない極限値pに収束するときには，初めの無限積はpに収束するといい，Пa_n＝pと書く。｛p_n｝が収束しないか，または0に収束するとき，無限積は発散するという。Пa_nが収束すればa_n→1であるが，逆は成立しない。無限積は，その項を1＋a_n（a_n→0）と書いてП（1＋a_n）の形で扱うのが便利である。П（1＋a_n）とΣlog（1＋a_n）とは同時に収束または発散する。a_n≧0ならばП（1＋a_n）とΣa_nとは同時に収束または発散する。無限積П（1＋｜a_n｜）が収束するとき，П（1＋a_n）は絶対収束するという。絶対収束する無限積の値は項の順序に関係しない。無限積の公式，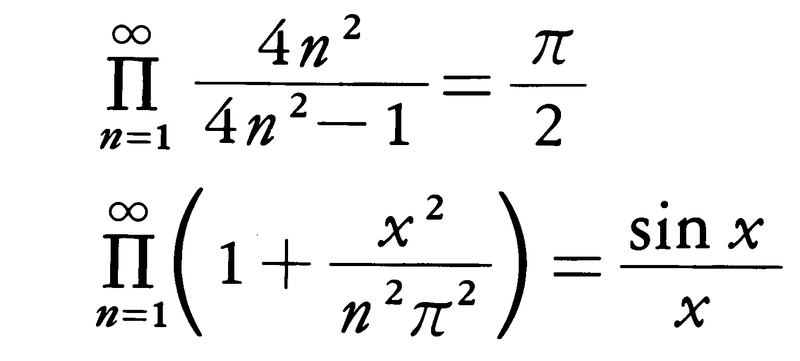

などは有名である。
→無限級数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

無限積
むげんせき

「無限乗積」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典