数列（読み）スウレツ（英語表記）sequence

デジタル大辞泉

すう‐れつ【数列】

１ 2、3か5、6ぐらいの列。いくつかの列。
２ ある一定の規則に従って順に並べられた数の列。おのおのの数を項という。

出典　小学館

精選版 日本国語大辞典

すう‐れつ【数列】

1. 〘 名詞 〙
2. ① 数の列。自然数１、２、３…に一つずつ数を対応させることによって得られる。終わりがあるかどうかにより有限数列または無限数列という。〔生物学語彙（1884）〕
3. ② 三～四列、五～六列ぐらいの列の数を、ばくぜんという語。
   1. [初出の実例]「蓮〈略〉辨萼各々数列あり」(出典：植物小学（1881）)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

数列 (すうれつ)
sequence

ある定まった規則に従って順次並べられた数の列を数列といい，数列の各数をその数列の項という。第n番目の項がa_nである数列を｛a₁，a₂，……，a_n，……｝，または｛a_n｝で表す。項の番号nに対応してa_nを定める規則が与えられれば，一つの数列が定義される。例えばa，d，rを定数とするとき，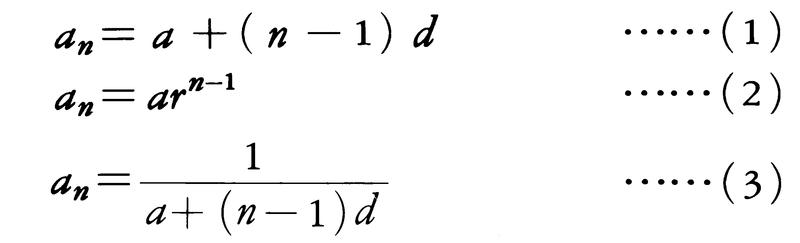

で定義される数列は，それぞれ等差数列，等比数列，調和数列と呼ばれる。また，a₁とa₂が与えられ，a_n＝1/2（a_n-1＋a_n-2）（n≧3）という規則が与えられれば，すべてのa_nが順次定まるから，一つの数列が定義される。

　数列の項の数が有限であるか無限であるかに従って，有限数列または無限数列という。単に数列といえば無限数列を指すことが多い。以下，本項目では無限数列のみを考える。

　数列｛a_n｝において，nが限りなく大きくなるとき，a_nが一つの定まった値cに限りなく近づくならば，この数列は極限値cに収束するといい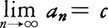，またはx_n→c（n→∞）と書く。もしも，nが限りなく大きくなるとき，a_nが限りなく大きくなるか，または－a_nが限りなく大きくなるならば，この数列はそれぞれ正の無限大に定発散する，または負の無限大に定発散するといい，このことを，それぞれ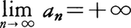または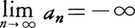と書く。その他の場合は，数列は不定発散する，または振動するという。定発散と不定発散とを合わせて単に発散という。例えば数列｛rⁿ｝については，｜r｜＜1ならば極限値0に収束し，r＝1ならば極限値1に収束し，r＞1ならば正の無限大に定発散し，r≦－1ならば不定発散する。

　数列｛a_n｝が，a₁≦a₂≦……≦a_n≦a_n+1≦……を満たすとき，この数列は単調増加であるといい，a₁≧a₂≧……≧a_n≧a_n+1≧……を満たすとき，この数列は単調減少であるという。この二つを総称して単調数列という。単調増加数列｛a_n｝において，a_nがnに無関係な一定の値より大きくならなければ，この数列は収束する。また，単調減少数列｛a_n｝において，a_nがnに無関係な一定の値より小さくならなければ，この数列は収束する。一般の数列の収束に関しては次の判定条件（コーシーの判定条件という）がある。数列｛a_n｝が収束するための必要十分条件は，mとnが互いに無関係に限りなく大きくなっていくとき，a_m－a_nが限りなく0に近づくことである。

　数列｛a_n｝に対してb_n＝a_n+1－a_nで定義される数列｛b_n｝をもとの数列の階差数列という。例えば｛1，4，9，……，n²，……｝の階差数列は｛3，5，……，2n＋1，……｝である。もとの数列｛a_n｝と階差数列｛b_n｝との間にはa_n＝a₁＋（b₁＋b₂＋……＋b_n-1）なる関係があるから，a₁と｛b_n｝から｛a_n｝が求められる。
→級数　→収束
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

数列
すうれつ

自然数1, 2, 3, 4,……のおのおのに対応して並べられた数の列a₁, a₂, a₃, a₄,……を数列という。そのおのおのの数を数列の項といい、初めから順に、初項、第2項、第3項、……という。数列の第n項をおのおのの項の代表と考えるとき、これを一般項という。一般項は、nの式として与えられることが多い。数列には、項が有限個で終わる有限数列と、どこまでも続く無限数列とがある。有限数列の最後の項を末項という。数列の例としては等差数列、等比数列などがよく扱われる。しかし、そのほかにも、いろいろな数列がある。

　数列a₁, a₂,……が与えられたとき初項から第n項までの和がよく問題になる。これを記号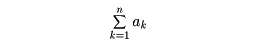

で表す。数列a₁, a₂,……を定めるのに、各a_nをそれより以前の項a₁, a₂,……, a_n-1の式として定めることがある。

　　a_n＝f(a₁, a₂,……, a_n-1)
このとき、この式を漸化式という。等差数列の漸化式は
　　a_n＝a_n-1＋d　（dは交差）
等比数列の漸化式は
　　a_n＝a_n-1r　（rは公比）
次の漸化式で表されるのがフィボナッチ数列である。

　　a₁＝1,　a₂＝1,　a_n＝a_n-1＋a_n-2
　　(n≧3)
　数列a₁, a₂,……に対して、
　　a_n⁽¹⁾＝a_n+1－a_n
　　(n＝1, 2,……)
によって定められる数列a₁⁽¹⁾, a₂⁽¹⁾,……を第一階差数列、
　　a_n⁽²⁾＝a_n+1⁽¹⁾－a_n⁽¹⁾
　　(n＝1, 2,……)
によって定められる数列a₁⁽²⁾, a₂⁽²⁾,……を第二階差数列といい、同様に第三階差数列、……という。数列の成り立ちを知るのに階差数列をつくって調べると役にたつことがある。

　無限数列が、先のほうにいくとどうなるかを論ずるのが数列の極限の議論である。無限数列を初項から順に加えていくとどうなるかを調べることがある。数列a₁, a₂,……を形式的にプラス記号で結んだa₁＋a₂＋……を級数という。

［竹之内脩］

[参照項目] | 級数 | 極限 | 収束 | 等差数列 | 等比数列

よく使われる数列の和

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

数列
すうれつ
sequence; progression

自然数の集合の元 n ( n＝1，2，3，… ) に，おのおの1つの実数 a_n を対応させて並べた数の列

a₁，a₂，a₃，…，a_p，…

を数列 (実数列ともいう) といい，これを記号で {a_n} あるいは {a_n} ( n＝1，2，3，…，p，… ) と書く。 n に a_n を対応させるという意味では，自然数から実数への関数とも考えられる。たとえば，自然数 1，2，3，…，p，… ，偶数 2，4，6，…，2p，… ，奇数 1，3，5，…，2p－1，… は，すべて数列である。数列において，第1番目，第2番目，…，第 p 番目の項を，それぞれ第1項 (初項) ，第2項，…，第 p 項などという。自然数に0を加える流儀もあり，それに伴って，a₀ ，a₁ ，a₂ ，… とすることもある。また，両側に広げて，整数からの関数　 … ，a_-2 ，a_-1 ，a₀ ，a₁ ，a₂ ，… 　を考えることもある。 (→極限値 ,　収束 ) 　

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

数列【すうれつ】

定まった規則に従い順序づけて並べられた数の系列。一つずつの数を数列の項といいn番目の項をa(/n)と書けば数列自身は｛a(/n)｝（n＝１，２，…）または単に｛a(/n)｝と書かれる。項の数が有（無）限なら有（無）限数列という。等差数列a(/n)＝a＋（n−１）d（dは公差），等比数列a(/n)＝ar(n/)(-/)¹（rは公比）等。→収束／級数
→関連項目発散（数学）

出典　株式会社平凡社

世界大百科事典（旧版）内の数列の言及

【級数】より

…ある規則に従って順次に並べられた数または関数の列を，それぞれ数列または関数列といい，それらの列を順次に加法記号で結合した式を級数という。例えば｛1,3,5,7，……｝，｛1,2,4,8，……｝は数列であり，これらに対応する級数は，それぞれ1＋3＋5＋7＋……，1＋2＋4＋8＋……である。…

※「数列」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」