直交関数（読み）ちょっこうかんすう（英語表記）orthogonal function

ブリタニカ国際大百科事典 小項目事典

直交関数
ちょっこうかんすう
orthogonal function

区間 [a，b] で定義されている2つの関数 f(x) ，g(x) が微分可能であるとき，もし
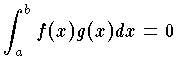であれば，f(x) と g(x) は [a，b] において直交するといい，直交する関数を直交関数という。区間 [a，b] で定義され，微分可能な実関数全体の集合はベクトル空間となる。このベクトル空間を V とし，その2つの元 f ，g の内積を ＜f，g＞ と書くことにすれば，簡単に
が導かれ，f(x) ，g(x) が直交関数であることを，＜f，g＞＝0 を満たす V の元 f ，g として定義することもできる。

出典　ブリタニカ国際大百科事典 小項目事典