集合（読み）シュウゴウ（その他表記）set

デジタル大辞泉

しゅう‐ごう〔シフガフ｜シユウガフ〕【集合／^×聚合】

［名］(スル)
１ 1か所に集まること。また、集めること。「駅前に八時に―する」⇔解散。
「森羅万象を―して自在に己れの材料と為し」〈鉄腸・花間鶯〉
２ 数学の基本概念の一。物の集まりで、個々の物がその集まりの中に属するかどうか、かつ、その集まりの中の二つの物が等しいかどうかが明確に判定できるものをいう。個々の物を元げんまたは要素という。
[類語]集結・結集・糾合・集まる・集う・群がる・群れる・屯たむろ・駆け付ける・殺到・すだく・たかる・固まる・参集・揃う・寄り合う・寄り集まる・寄り集う・馳せ集まる・馳せ参ずる・馳せつける・勢揃い・オンパレード・集中・集散・凝集・密集・蝟集いしゅう・群集・集積・離合・拡散・分散・四散・散開・飛散・雲散・離散・霧散・散逸・雲散霧消

出典　小学館

精選版 日本国語大辞典

しゅう‐ごうシフガフ【集合・聚シュウ合】

1. 〘 名詞 〙
2. ① ( ━する ) いくつかのものが一か所に集まること。〔布令必用新撰字引（1869）〕
   1. [初出の実例]「風俗の情形は家風の聚合（〈注〉アツマル）するものにして」(出典：西国立志編（1870‐71）〈中村正直訳〉一二)
   2. [その他の文献]〔爾雅疏‐釈詰〕
3. ② ( ━する ) いくつかのものを一か所に集め合わせること。寄せ合わせること。
   1. [初出の実例]「上法を反覆して消石瓦斯を以て諳摸尼亜を集合す」(出典：舎密開宗（1837‐47）内)
   2. [その他の文献]〔漢書‐劉向伝〕
4. ③ 数学の基礎概念の一つ。物の集まりで、任意の物がこの集まりに属しているか否かの判定ができ、かつ、この集まりの中の二つのものを取り出すとき、それらが等しいか否かの判定がつくような物のこと。集合に属する個々の物をその要素、元素、元などという。
5. ④ 結合して一つの塊をなした鉱物の結晶。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

集合 (しゅうごう)
set

数学で記述を整理し明確化するために，19世紀後半に導入された概念。素朴には，〈思考の対象として明確な意味をもつもので指定した範囲内にあるものを集めたものを集合といい，その集められたものをその集合の元または要素という〉といえばよいが，多少の補足が必要である。

　まず，われわれは物を区別したり，まとめたり，ときに応じて適宜処理している。例えば分数1/2と小数0.5とは，数としては同じであるが表記としては別であるから，1/2と0.5とを同じと考えるときと別と考えるときとがある。そこで，〈数としての1/2〉〈数の大きさと表記とを併せ考えた1/2〉〈単なる記号としての1/2〉など，いろいろ考えられるが，集合の元として考える場合，どういう意味の1/2かを初めに確定しておかなくてはならない。三つを互いに異なる元として，同じ集合に属させてもよい。このことが上にいう〈明確な意味をもつ〉に含まれているのである。他方，〈集合論〉の項目で述べるように，上の定義は論理的にも欠点がある。

基本概念と記号

aが集合Mの元であるときaはMに属するともいう。a∈MまたはM∋aのように∈，∋で表す。その否定（aがMの元ではないこと）には/，｜，，￣のいずれかを加えた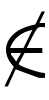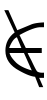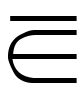，∉，，または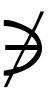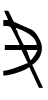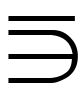，，，を用いる。否定の記号はまだほかにもあり，また，∈に限らず，いろいろな場合の否定に同様に使われるので，今後本稿では，否定には｜を加えたものを使うことにする。

　二つの集合M，Nについて，

（1）Mの元は必ずNの元でもあるとき，MはNの部分集合であるといい，M⊆N，N⊇M，M⊂NまたはN⊃Mで表す。

（2）M⊆NかつN⊆Mのとき，すなわち，Mの元全体とNの元全体とが同じであるとき，MとNとは同じ集合であると考え，M＝Nで表す。

（3）M⊆NかつM≠Nのとき，MはNの真部分集合であるといい，M⊂N，N⊃MまたはM⊊N，N⊊Mで表す。

　包含関係の記号⊆，⊂は上の説明からわかるように，少し混乱している。

（1）部分集合に⊆，真部分集合に⊂を使うのが一つの行き方である。

（2）部分集合に⊂，真部分集合に⊊を使う人も多くいる。

　⊂の意味があいまいになるのをおそれる人は，

（3）部分集合に⊆，真部分集合に⊊を使うようになっている。

　集合を示すのに，｛　｝の中に元を書き示すことが多い。｛a｝，｛b，c｝はそれぞれa;b，cを元とする集合である。また｛x｜0＜x＜1｝は0＜x＜1を満たす数x全体の集合である。一般に集合Mの元に関する条件Pがあるとき，条件Pを満たすMの元全体の集合を｛x∈M｜P｝のように，｛　｝の中に｜（文献によっては;）を入れ，その右側に条件を書き入れて表す。∈Mは略すこともある。

　元をまったく含まない集合も考え，それを空集合という。空集合を表すのにはØ，Φ，φなどの記号が用いられる（0に似て非なるものということで0に/をつけてØが最初に用いられ，Φはその変形，φはΦに似たギリシア文字による代用）。

　A，Bが集合Mの部分集合であるとき，

｛x∈M｜x∈Aかつx∈B｝をAとBの共通部分または交わり，まれには積集合といい，A∩Bで表す。｛x∈M｜x∈Aまたはx∈B｝をAとBの合併集合または和集合といい，A∪Bで表す。共通部分，合併集合などを考えるとき，図のように集合を象徴的に表すと便利なことがある。このような図をベン図またはベンJ.Venの図式という。

　Aが集合Mの部分集合であるとき，｛x∈M｜x∉A｝をAのMにおける補集合といい，A^c，M－A，MA，Aなどの記号で表されることが多い。また，“Mにおける”は省略されることが多い。

　多くの部分集合A₁，……，A_nの共通部分，合併集合についても同様であり，

　A₁∩……∩A_n＝｛x｜すべてのi＝1，2，……，nについて，x∈A_i｝。これを

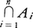とも書く。

　A₁∪……∪A_n＝｛x｜あるiについて，x∈A_i｝。これを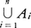とも書く。

あるいは，集合Sで番号づけられた部分集合A_σ（σ∈S）が与えられたとき，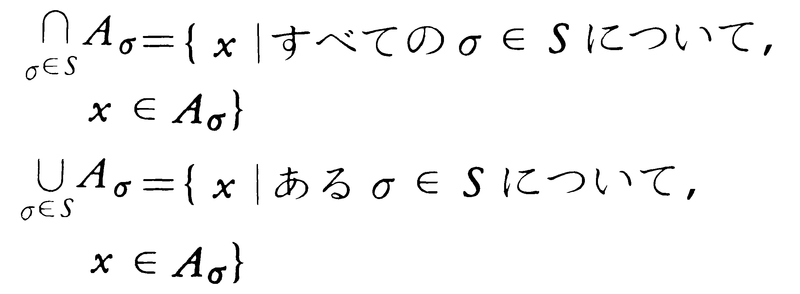

　A，B，Cが集合Mの部分集合であるとき，次の等式が成り立つ。

（1）交換法則　A∩B＝B∩A

　　　　　　A∪B＝B∪A

（2）結合法則　（A∩B）∩C＝A∩（B∩C）＝A∩B∩C

　　　　　　（A∪B）∪C＝A∪（B∪C）＝A∪B∪C

（3）分配法則　A∩（B∪C）＝（A∩B）∪（A∩C）

　　　　　　A∪（B∩C）＝（A∪B）∩（A∪C）

（4）吸収法則　A∪（A∩B）＝A

　　　　　　A∩（A∪B）＝A

（5）ド・モルガンの法則

　　　　　　（A∩B）^c＝A^c∪B^c

　　　　　　（A∪B）^c＝A^c∩B^c

もっと一般に，Sで番号づけられた部分集合N_σについて，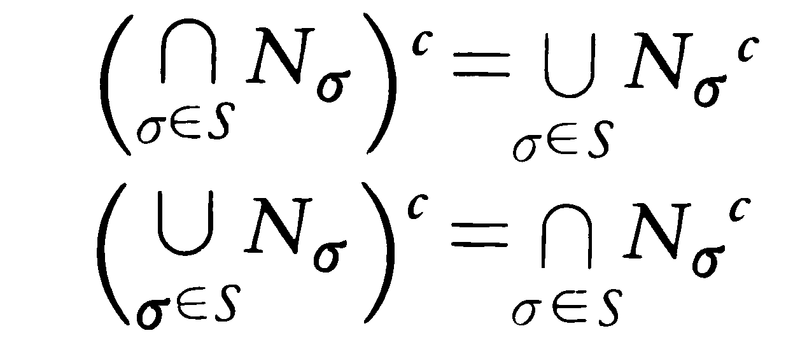

ド・モルガンの法則は，一つの集合の部分集合についての⊆，⊇，＝，∩，∪を使った関係式は，各部分集合をその補集合に置きかえ，＝はそのままにして，⊆と⊇とを取りかえ，∩と∪とを取りかえたものと同値であることを示している。これを集合算の双対性という。ここで，集合算というのは，∩，∪を集合間の演算と考えたことをいうのである。

直積

二つの集合A，Bが与えられたとき，Aの元とBの元の組の集合｛（a，b）｜a∈A，b∈B｝をAとBの直積（または直積集合）といい，A×Bで表す。これは集合｛1，2｝から，A∪Bの中への写像fで，f（1）∈A，f（2）∈Bを満たすものの全体Tを取ると，Tの元fとA×Bの元（f（1），f（2））との対応によって，TとA×Bとの1対1対応が得られる。そこで，この対応でTとA×Bとを同一視することにする。そして，無限個の集合の場合を含めて，直積を次のように定義する。集合Sで番号づけられた集合A_σ（σ∈S）の集りがあるとき，Sから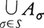の中への写像fで，各σ∈Sに対してf（σ）∈A_σを満たすもの全体の集りをA_σ（σ∈S）の直積といい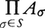，で表す。有限個の集合A₁，A₂，……，A_nの直積は，A₁×A₂×……×A_nと書いてもよく，これは｛（b₁，……，b_n）｜b_i∈A_i（i＝1，2，……，n）｝であると考えてよい。

　一般のSについて，B＝A_σがすべてのσ∈Sについて成り立つとき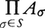，をB^sともかく。すなわち，B^sはSからBの中への写像全体である。

濃度

集合に属する元の多さを示す概念に濃度（またはカージナル数）と呼ばれるものがある。集合Mの濃度は，♯（M），｜M｜，Card Mなどの記号で表されるが，それは次のように定義される。（1）Mが有限個の元しかもたないとき，Mは有限集合と呼ばれ，♯（M）はMの元数であると定める。このような濃度を有限の濃度という。（2）有限集合でない集合を無限集合といい，その濃度を無限の濃度という。（3）一般に，二つの集合A，Bについて，♯（A）と♯（B）との大小関係を次のように定める。（a）AからBの中への単射f（すなわち，AからBの中への写像fで，a，a′∈A，a≠a′ならばf（a）≠f（a′）という性質をもつもの）があるとき，すなわち，AとBのある部分集合B′との間に1対1対応があるとき，♯（A）≦♯（B）（♯（B）≧♯（A））と定める。（b）AとBとの間に1対1対応があるとき，♯（A）＝♯（B）と定める。（c）♯（A）≦♯（B）かつ♯（A）≠♯（B）のとき，♯（A）＜♯（B）（♯（B）＞♯（A））と定める。すると，ベルンシュタインF.Bernstein（1878-?）の定理〈二つの濃度♯（A），♯（B）の間には次の三つのうちちょうど一つが成り立つ。♯（A）＜♯（B），♯（A）＝♯（B），♯（A）＞♯（B）〉が成立するので，濃度の大小関係がうまく定義されることになるのである。

　濃度について，次のような演算が考えられている。（1）A∩Bが空集合のとき，♯（A）＋♯（B）＝♯（A∪B），（2）♯（A）×♯（B）＝♯（A×B），（3）♯（A）^♯⁽^b⁾＝♯（A^b），この演算については，♯（A）＋♯（B）＝♯（B）＋♯（A），♯（A）×♯（B）＝♯（B）×♯（A），♯（A）^♯⁽^b⁾⁺^♯⁽^c⁾＝♯（A）^♯⁽^b⁾×♯（A）^♯⁽^c⁾が成り立つ。有限の濃度のときは数としての加法，乗法，べき乗と同じとみなせるが，無限の濃度についてはだいぶようすが違う。例えば，Aが無限集合であれば，♯（A）×♯（A）＝♯（A）である。一般の場合のこの等式の証明はむずかしいが，Aが自然数全体の集合のときは，次のようにして証明される。A×A＝｛（m，n）｜m，nは自然数｝の元を次のように順次並べていく。（1，1），（2，1），（1，2），……，（n，1），（n－1，2），……，（n－r，r＋1），……，（1，n），……。すると，（a，b）は1/2（a＋b－2）（a＋b－1）＋b番目に並ぶことになり，（a，b）に1/2（a＋b－2）（a＋b－1）＋bを対応させることによって，A×AとAとの1対1対応が得られる。また，この等式♯（A）×♯（A）＝♯（A）から次のこともわかる。すなわち，♯（A）が無限の濃度，♯（A）≧♯（B）＞0ならば，♯（A）×♯（B）＝♯（A）である。

べき集合

集合Mの部分集合全体のなす集合Pを，Mのべき集合という。Pの濃度は2^♯⁽^m⁾であり，このことは，Mの各部分集合Aに対して，その特性関数，すなわち，M上次のように定義された関数f_a［a∈Aならf_a（a）＝1，a∉Aならf_a（a）＝0］を対応させれば，Pと｛0，1｝^aとの1対1対応になることからわかる。この濃度について，次のカントルの定理がある。〈どんな集合Mについても，2^♯⁽^m⁾＞♯（M）である〉（対角線論法）。

可算無限と連続体の濃度

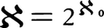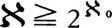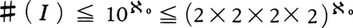
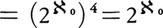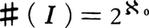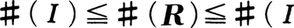
無限の濃度のうち最小のものは自然数全体の集合Nの濃度である。これを可算無限（または可付番無限）の濃度と呼ぶ。以下これをℵ₀（ℵはヘブライ文字アレフ）で表そう。実数全体の集合Rの濃度を連続体の濃度という。これをℵで表せば，である。なぜならば，｛0，1｝ⁿの元fに対し，小数0.f（1）f（2）……f（n）……（小数点以下n位の数字がf（n））を対応させれば，｛0，1｝ⁿとI＝｛x∈R｜0≦x＜1｝の部分集合で，小数展開で表れる数字が0か1に限るもの全体との1対1対応が得られるから，。Iの元の小数展開を考えると，｛0，1，……，9｝ⁿの元のうち，あるN以上のnすべてについて，f（n）＝9となる元を除いた集合とIとの1対1対応が得られるので，（無限の濃度についての等式♯（A）×♯（A）＝♯（A）による）。ゆえに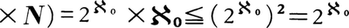，。ゆえ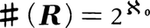，となる。したがって，カントルの定理により，ℵ＞ℵ₀。また，ℵ²＝ℵゆえ，ℵⁿ＝ℵ（n＝1，2，……）であり，n次元ユークリッド空間（n＝1，2，……）の点全体の集合の濃度もℵである。

　正の有理数に対して，それを既約分数で表したときn/mであれば，N×Nの元（m，n）を対応させてみれば，正の有理数全体Q⁺について，♯（N）≦♯（Q⁺）≦♯（N×N）＝♯（N）が得られ，有理数全体 Qの濃度もℵ₀であることがわかる。したがって，無理数全体Sの濃度については，ℵ＝♯（S）＋ℵ₀≦♯（S）×ℵ₀＝♯（S）であるから，Sの濃度もℵであり，無理数は有理数に比べて格段に多く存在することがわかる。

整列集合

自然数全体の集合Nは，〈空でない部分集合Sを取れば，Sにはもっとも小さい数がある〉という性質をもっている。このことを一般化した次の性質をもつ順序集合Wを整列集合という。〈SがWの空でない部分集合であれば，Sには最小元がある〉。

　a，b∈Wのとき｛a，b｝に最小元があるのであるから，上の条件はWが全順序集合であることを含んでいる。

　整列集合の部分集合は整列集合であるから，Nおよびその部分集合により，簡単な整列集合の例が得られるが，多少複雑な例としては，次の定理においてA_i＝N（i＝1，2，……，n）の場合がある。

　定理　A₁，A₂，……，A_nが整列集合であれば，直積A₁×A₂×……×A_nは辞書式順序によって整列集合になる。

　ここで辞書式順序は次のように定義する。（a₁，a₂，……，a_n）＞（b₁，b₂，……，b_n）は，a₁＞b₁またはa₁＝b₁かつa₂＞b₂，……，またはa_i＝b_i（i＝1，……，r）かつa_r+1＞b_r+1，……，またはa_i＝b_i（i＝1，……，n－1）かつa_n＞b_nのときと定める。

　なお，二つ以上の元をもつ整列集合A₁，A₂，……，A_n，……（無限個）があるとき，これらの直積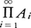に辞書式順序を入れたものは整列集合にはならない。それは，各A_iから二つずつ元a_i，b_i（a_i＞b_i）を選び，c₀＝（a₁，a₂，……，a_n，……），c₁＝（b₁，a₂，a₃，……，a_n，……），……，c_r＝（b₁，b₂，……，b_r，a_r+1，a_r+2，……，a_r+n，……），……を考えると，c₀＞c₁＞c₂＞……＞c_r＞c_r+1＞……となり，｛c_i｜i＝0，1，2，……｝に最小元がないからである。

　次の定理はE.ツェルメロによって証明されたものであり，整列可能定理と呼ばれる。〈どんな集合Mに対しても，それに適当な順序を与えて整列集合にすることができる〉。

順序数

一般に二つの順序集合M，Nが同型であるとは，MからNへの1対1対応（全単射）fであって〈a＞b⇔f（a）＞f（b）〉の成り立つものが存在するときにいう。例えば，自然数全体の集合Nを考えると，｛2n｜n∈N｝とNは同型であり，NとN×N（辞書式順序による）とは同型ではない。

　整列集合Wとその元aが与えられたとき，｛x∈W｜x＜a｝をWのaによる切片という。以下W〈a〉で表すことにする。すると，次の定理が成り立つ。

　定理　W，Uが整列集合であれば，次の三つのうち，きっかり一つだけが成り立つ。（1）WとUとは同型，（2）WはUのある切片と同型，（3）UはWのある切片と同型。〈きっかり一つだけ〉ということから，この定理は，WはWの切片とは決して同型でないことも含んでいる。

　そこで順序数（順序型ともいう）を，濃度の場合と似た形で，次のように定める。

（1）同型な整列集合は同じ順序数を対応させる。

（2）WがUの切片と同型である場合には，Wに対応する順序数wはUに対応する順序数uより小さいと定める。

　なお，m個の元からなる整列集合は｛1，2，……，m｝と同型であり，これに対応する順序数はmで表すのがふつうである。有限でない順序数のうち最小であるものは自然数全体の集合Nに対応するものであり，ωで表されることが多い。

　このように定義すると，次の定理が成り立つ。

　定理　γが順序数であれば，γより小さい順序数全体Γは整列集合をなし，Γに対応する順序数はγと一致する（γ∉Γに注意せよ）。

　二つの順序数α，βの和α＋βは次のように定義される。対応する順序数がそれぞれα，βであるような整列集合A，BをA∩Bが空集合であるように取り，A∪Bにおいて，x∈A，y∈Bならばx＜yであるものと定めると，A∪Bは整列集合になる。このとき，A∪Bに対応する順序数がα＋βであると定める。

　この加法では，α＋β＝β＋αとは限らない。例えばω＋1はN∪｛∞｝に対応すると考えてよく，それは最大元∞をもつからNとは同型でない。しかし，｛0｝∪NはNと同型になるから，1＋ω＝ω＜ω＋1。

　♯（N）＝♯（N×N）であるのに，N×Nに対応する順序数はω，ω＋ω，ω＋ω＋ω，……のいずれよりも大きいことからわかるように，一つの無限の濃度に対して，同じ濃度をもちながら同型でない整列集合は無限に多くある。すなわち，各順序数αに対し，対応する整列集合の濃度（これをαの濃度という）を対応させることができるが，この対応は，（1）有限の順序数に対しては1対1の対応であるが，（2）ω以上の順序数に対しては無限対1の対応になる。

ツォルンの補題

存在証明にしばしば使われる定理にツォルンM.A.Zornの補題がある。文献によっていろいろな形で述べられているが，その一つは次のように述べられる。

　〈順序集合Mにおいて，Mのどんな空でない整列部分集合Sについても，Sの上限sup SがMの中に存在するならば，Mには少なくとも一つの極大元がある〉。

　ここで，aがSの上限であるとは，aがSの上界全体のうちの最小元（すなわち，s∈Sならば，a≧sであり，b∈Mかつすべてのs∈Sについてb≧sならばb≧a）であることを意味する。また，mがMの極大元であるとは，x＞mであるようなMの元xは存在しないときにいう。

　応用例1　群Gの部分集合Sが単位元を含まないとき，Gの部分群でSと共通元をもたないもの全体Fのうちには，包含関係の意味で極大なものがある。

　証明　F中の整列部分集合｛H_λ｜λ∈Λ｝（Λは整列集合で，λ，μ∈Λ，λ＜μならばH_λ⊊H_μ）に対して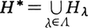，を考えると，これは部分群であり，H^＊⊇H_λがすべてのλについて成り立つ。あるH∈Fについて，H⊇H_λがすべてのλについていえれば，H⊇∪H_λであるから，H^＊は｛H_λ｜λ∈Λ｝の上限である。ゆえにツォルンの補題により，Fに極大元が存在する。

　応用例2　実数全体Rを有理数体Q上の加群と考えたとき，一次独立基Bがある。

　ここで，Rの部分集合Bが一次独立基であるとは，（1）Bの有限個の元b₁，……，b_nが互いに異なれば，b₁，……，b_nはQ上一次独立であり，（2）Rのどの元αも，適当なBの元b₁，……，b_nと有理数r₁，……，r_nとにより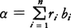，と書けることを意味する。

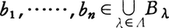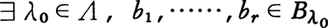　証明　Rの部分集合Bで一次独立なもの（上の（1）を満たすもの）全体Fを考える。部分集合の包含関係によりFを順序集合と考えると，Fの中の整列集合｛B_λ｜λ∈Λ｝があれば，ならば，ゆえ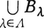，もFに含まれる。ゆえにツォルンの補題により，Fには極大元B^＊がある。B^＊の元b₁，……，b_nおよび有理数r₁，……，r_nをどのように選んでも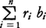，の形では表しえない実数sがあれば，B^＊∪｛s｝も一次独立になり，B^＊の極大性に反する。ゆえにB^＊はRの一次独立基である。

点集合

ユークリッド空間は点の集りであり，この意味での部分集合を扱うのを点集合論という。この立場の集合は単なる点の集りとしての集合ではない。ユークリッド空間を距離空間と考えて，その意味での位相や，長さ，面積，体積などを考慮に入れて考えたものである。したがって，多くの事柄が位相空間論へと一般化される。

　以下，n次元ユークリッド空間（n≧1）E＝Rⁿの中で考える。2点p，qの座標が（p₁，p₂，……，p_n），（q₁，q₂，……，q_n）であるとき，p，qの距離d（p，q）は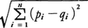として定義する。εが正の数であるとき，点pのε近傍は｛q∈E｜d（p，q）＜ε｝と定める。

　点pが集合Sの集積点であるとは，どんな正の数εによるpのε近傍U_ε（p）を取っても，U_ε（p）とSとが必ずp以外に共通点をもつときにいう。さらに，U_ε（p）∩Sの濃度が必ず非可算の濃度であるとき，pはSの凝集点という。集合Fについて，〈pがFの集積点ならばp∈F〉が成り立つとき，Fは閉集合であるという。集合Sにその集積点を全部併せた集合Sを作ると，これはSを含む最小の閉集合になる。これをSの閉包という。集合Sの点pで，適当に正の数εを取ればpのε近傍がSに含まれてしまうものを，Sの内点という。閉集合の余集合であるような集合を開集合という。Uが開集合であるとは，〈p∈Uならば，pはUの内点である〉という条件で特徴づけられる。集合Sの内点全体は開集合になる。これをSの開核という。

　集合Sが有界であるとは，適当な点pと十分大きい実数rを取れば，pのr近傍U_r（p）がSを含んでしまうときにいう。有界閉集合はコンパクトであるというのはユークリッド空間のたいせつな性質である。

　集合Sの点pについて，適当な正の数εを取れば，U_ε（p）∩S＝｛p｝となるとき，pはSの孤立点であるという。

　集合Sに対し，Sの集積点全体のなす集合をSの導集合という。それがSと一致するとき，Sは完全集合であるという。

　次に示すカントル集合は，（1）完全集合であって，（2）内点をもたず，（3）どんな正数εを与えても，長さの和がε以内であるような線分で覆うことができるということから，長さ0と考えられ，（4）濃度は連続体の濃度であるということで有名である。

カントル集合

カントルの三進集合とも呼ばれ，次のように定義される。一般に，a，bが実数でa＜bのとき，［a，b］および（a，b）はそれぞれ｛x｜a≦x≦b｝，｛x｜a＜x＜b｝を表すものとし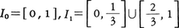，を考える。

すなわち，I₁はI₀から1/3の長さの開区間を中央から取り去ったものである。同様に，I₁の二つの線分（閉区間）から，それぞれの1/3の長さの開区間を中央で取り去ったものをI₂とする。すなわち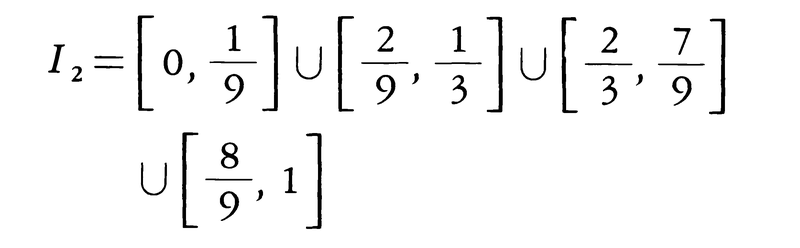

以下同様にして，長さ3⁻ⁿの開区間2ⁿ個の和集合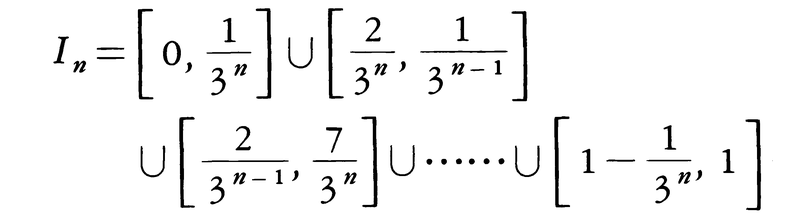

を得る。これは，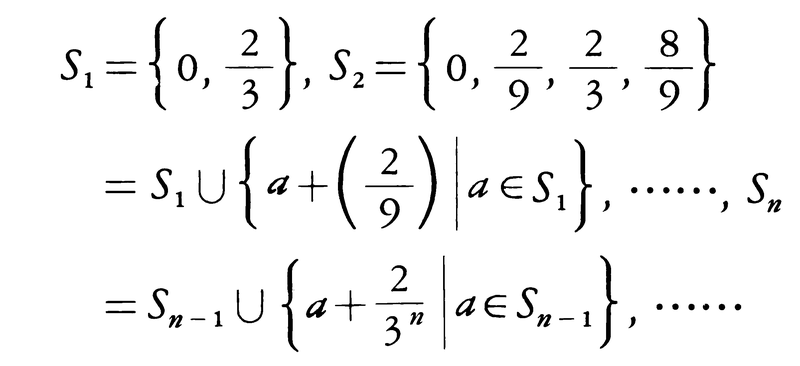

とおけば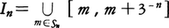，である。このとき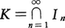，をカントル集合という。

　この集合は，三進小数展開を使うと見やすい。a∈［0，1］を三進小数展開して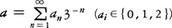であるとき，a∈I_nの条件はa₁，a₂，……，a_nに1が現れないことである。したがって，a∈K⇔≏a_n∈｛0，2｝。このことから，Kの濃度は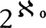すなわち連続体の濃度であること（上記（4））がわかり，また上記（1）もこのことから容易にわかる。各I_nの線分の長さの和は\(\frac{2^n}{3^n}\)であるから，上の（3）がわかり，したがって（2）もわかる。
執筆者：永田 雅宜

図－集合

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

集合
しゅうごう

教室の机や椅子(いす)とか、1から50までの自然数のようにはっきり定義されたものを一つの全体として考えたものを、それらの対象の集合といい、それらの対象をその集合の元(げん)とか要素という。aが集合Aの元であることをa∈Aと書き、aはAに属するとか、Aはaを含むという。集合をつくる対象は、机や椅子のように実在しているものでもよいし、頭のなかで架空的に考えられたものでもよい。有限個の元からできている集合を有限集合という。それに対して、自然数1、2、3、……の全体、直線上の点の全体はいずれも集合であるが、これらの集合はその元を数えきることができない。このような無限個の元を含む集合を無限集合という。集合の元の個数を濃度という。一つの集合を定義するのには2通りの方法がある。一つは、集合の要素をa、b、c、……のように列記する方法である。この集合を｛a, b, c,……｝と書く。もう一つは、ある性質が与えられたとき、その性質をもっているもの全体を一つの集合とする方法である。「nは自然数である」という性質をもつnの全体は自然数全体の集合ということになる。その性質をもつような対象がないとき、この性質は、元を一つも含まない集合を与えることになる。元をまったく含まない集合を空集合(くうしゅうごう)といい、しばしば∅という記号で表す。二つの集合AとBについて、Aのどの元も同時にBの元であるとき、集合Aは集合Bの部分集合であるといい、A⊂Bと書く。どの集合Aについても∅⊂Aである。AがBの部分集合(A⊂B)で、同時にBがAの部分集合(B⊂A)であるとき、すなわちAとBの元が同じとき、AとBは等しいといい、A＝Bと書く。

［西村敏男］

集合演算

AとBを集合とするとき、AかBの少なくとも一方に属する元の全体をAとBの和集合とか合併集合といい、A∪Bと書く（図の①）。AとBの両方に属する元の全体をAとBの共通集合といい、A∩Bと書く（図の②）。A＝｛1, 2, 3, 4｝、B＝｛2, 3, 5｝のとき、A∪B＝｛1, 2, 3, 4, 5｝、A∩B＝｛2, 3｝である。ある集合Uの部分集合だけを考えるとき、集合Uを全体集合という。たとえば、実数の集合だけを考えるときには、実数全体の集合が全体集合であり、平面上の点集合だけを考えるときは、平面上の点全体の集合が全体集合である。Uを全体集合とし、Aをその部分集合とする。Aに属さないUの元の全体をAの補（余）集合といい、A′などと書く（図の③）。このとき次の関係が成り立つ。

(1) A∪A′＝U, A∪∅＝A
(2) A∪A＝A（吸収法則）
(3) A∪B＝B∪A（交換法則）
(4) (A∪B)∪C＝A∪(B∪C)（結合法則）
(5) A∩(B∪C)＝(A∩B)∪(A∩C)（分配法則）
(6) (A∪B)′＝A′∩B′（ド・モルガンの法則）
また次の関係も成り立つ。

(1)′A∩A′＝∅, A∩U＝A
(2)′A∩A＝A
(3)′A∩B＝B∩A
(4)′(A∩B)∩C＝A∩(B∩C)
(5)′A∪(B∩C)＝(A∪B)∩(A∪C)
(6)′(A∩B)′＝A′∪B′
これら2組みの演算法則(k)と(k)′の間には次の関係がある。すなわち、(k)の記号∩、∪、U、∅をそれぞれ∪、∩、∅、Uで置き換えると(k)′になる。またこの逆も成り立つ。これを双対の原理(そうついのげんり)という。二つの集合AとBについて、a∈Aでb∈Bである対(a, b)の全体をAとBの（直）積集合といい、A×Bと書く。A＝｛1, 2｝、B＝｛a, b, c｝であるとき、
　　A×B＝｛(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)｝
である。XとYをともに実数全体の集合とするとき、X×Yは、実数s、tの対(s, t)の全体となり、これは平面上の点の全体の座標の集合と考えることができる（図の④）。集合Aの部分集合の全体からなる集合をAのべき集合という。A＝｛1, 2｝のとき、Aのべき集合は｛∅,｛1｝,｛2｝,｛1, 2｝｝である。

［西村敏男］

『小林善一著『算数と集合』（1972・東洋館出版社）』▽『矢野健太郎著『集合』（1973・共立出版）』▽『ヴィレンキン著、柴岡泰光訳『集合の話』（1975・東京図書）』▽『細井勉著『集合・論理』（1982・共立出版）』

[参照項目] | 集合論

集合〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

集合
しゅうごう
set

数学でいう集合とは，次の 2条件を満たす，直観または思考の対象となる物の集りを一つの対象としてまとめたもののことである。(1) 集合に入っている個々の物は，みな異なっている。すなわち，その集合から二つの物を取出すと，相等しいかあるいは相異なるかが識別できる。(2) 考えている範囲における任意の物は，考えている集合に入っているか入っていないかのいずれか一方であることが決定できる。すなわち，ある物がその集合に入っているかどうかを識別することができる。ただし，このように集合の「定義」を漠然と考えていると，ラッセルの逆理のような矛盾が生じる。それで，きっちりした数学として集合論を考えるときは，集合を無定義術語として公理系を立てて論じる。集合をつくっている個々の対象物を，集合の元あるいは要素といい，a が集合 A の元であることを a∈A または A∋a と書き，「a は A に属する」または「A は a を含む（a は A に含まれる）」と読む。また a が集合 A の元でないことを a∉A または A∌a で表わし，「a は A に属さない」または「A は a を含まない」と読む。集合のことを空間，元を点ということもある。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

集合

ものの集まりを集合といい、集合に入る要素を元という。集合という時には、ある要素がその集まりの中に含まれているかどうかを明確に区別できなければならず、いわば〇×の世界である。19世紀にカントール(G.Cantor)は集合論を誕生させ、無限にも量的な違いがあることを認識し、濃度という概念を導入した。自然数全体の集合は無限個の元を含むが、その元は1、2、3、4……というようにどこまでも並べていくことができる。このような無限を可算濃度という。整数全体の集合、有理数全体の集合、代数的数全体の集合も可算濃度である。カントールは、実数全体の集合がこのように並べられないことを示した。この濃度を連続体濃度といい、可算濃度よりも大きな濃度になる。複素数全体の集合も連続体濃度である。一方、世の中には〇か×ではない現象が多い。例えば、気温は暑い、寒いの2種類ではなく、少し暑いや少し寒いなどの中途半端な状態が存在する。このように、〇×の世界ではない「あいまいさ」を扱うために考案されたのが、1965年にザデー(L.A.Zadeh)によって発表されたファジー集合の理論。ファジー理論は、制御、パターン認識、人工知能などへの幅広い応用が考えられている。

(桂利行 東京大学大学院教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

百科事典マイペディア

集合(数学)【しゅうごう】

ある明確に定まった条件に適するものの集り。集合を構成する個々のものを要素または元という。要素が有限個なら有限集合，無限個なら無限集合，要素を全く含まない集合を空集合という。要素aが集合Aの要素であることをa∈Aで表す。集合A，BでAの要素はすべてBの要素であれば，AをBの部分集合といい，A⊂Bと書く。A，Bどちらかに属する要素からなる集合をA，Bの和集合または合併集合（記号A∪B），A，Bどちらにも属する要素からなる集合をA，Bの積集合または共通集合（記号A∩B）という。→集合論
→関連項目曲面｜元（数学）｜点

出典　株式会社平凡社

岩石学辞典

集合

→砕屑物

出典　朝倉書店

栄養・生化学辞典

集合

　→凝集

出典　朝倉書店

世界大百科事典（旧版）内の集合の言及

【集合論】より

…集合として扱われるものを使った推論。集合という概念を定義することを提案し，有効な理論を打ち立てたのはG.カントルである。…

※「集合」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」