関数y=f(x)の値がxの変化に従ってどのように変わるかを調べようとする。例えば,xがaからbまで変化する間にyはf(b)-f(a)だけ変化し,このyの変化とxの変化との割合は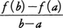 である。これらの値を調べるだけでも関数f(x)のだいたいのようすはわかるが,もっとくわしくf(x)の状態を知るためには,例えばx=aのときの〈瞬間的変化〉の状態を調べる必要が起こる。この瞬間的な変化の考えを数学的に厳密に定式化すると,すぐ後に説明するところの微分係数,導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。微分法のことを単に微分ということが多いが,これは〈微分することdifferentiation〉からきた略称である。本項では,微分法の具体的計算法やそのための公式,導関数のおもな性質やその応用について述べるので,項目名は微分法とすべきであろうが,微分の略称が一般に広く使われているのでこの略称を項目名とした。数学用語としての微分の本来の意味は,この項目中で後ほど〈微分〉という見出しで述べる。なお,微分係数を微分と呼ぶこともあるが,これは正しい用語ではない。微分法の初歩は多項式で表される関数の微分法であり,そのような関数を初等数学では整関数と呼ぶので,本項中でもこの名称を用いる。現代の数学では,整関数といえば複素平面全体で定義された正則な関数を意味する。また,多項式の比の形に表される関数を有理関数という。なお,〈関数〉〈関数論〉〈極限〉〈収束〉〈初等関数〉〈連続関数〉などの項を参照されたい。
である。これらの値を調べるだけでも関数f(x)のだいたいのようすはわかるが,もっとくわしくf(x)の状態を知るためには,例えばx=aのときの〈瞬間的変化〉の状態を調べる必要が起こる。この瞬間的な変化の考えを数学的に厳密に定式化すると,すぐ後に説明するところの微分係数,導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。微分法のことを単に微分ということが多いが,これは〈微分することdifferentiation〉からきた略称である。本項では,微分法の具体的計算法やそのための公式,導関数のおもな性質やその応用について述べるので,項目名は微分法とすべきであろうが,微分の略称が一般に広く使われているのでこの略称を項目名とした。数学用語としての微分の本来の意味は,この項目中で後ほど〈微分〉という見出しで述べる。なお,微分係数を微分と呼ぶこともあるが,これは正しい用語ではない。微分法の初歩は多項式で表される関数の微分法であり,そのような関数を初等数学では整関数と呼ぶので,本項中でもこの名称を用いる。現代の数学では,整関数といえば複素平面全体で定義された正則な関数を意味する。また,多項式の比の形に表される関数を有理関数という。なお,〈関数〉〈関数論〉〈極限〉〈収束〉〈初等関数〉〈連続関数〉などの項を参照されたい。
変化率(微分係数)などを解説する前に,以下の記述に必要な直線上の区間,近傍などの用語を説明しておく。数直線上でa≦x≦b,a<x<b,a≦x<b,a<x≦bなるxの範囲をそれぞれ[a,b],(ab),[a,b),(a,b]で表し,これらを区間と呼ぶ。とくに[a,b]なる形の区間を閉区間,(a,b)なる形の区間を開区間という。また実数aを与えたとき,任意の正数δに対して,(a-δ,a+δ)なる形の開区間をaの近傍という。これは直線上で考えた近傍である。もっと一般的な近傍の定義については,〈近傍〉〈位相空間〉などの項目を参照されたい。
変化率,微分係数,導関数
静止していた物体が落下し始めてからt秒間に落ちる距離をs(m)とすると,空気の抵抗を無視できるときは,s=4.9t2という関係がある。したがって,物体が落下し始めてからa秒後からb秒後までの(b-a)秒間に落下する距離は,4.9(b2-a2)mであり,その間の平均の速さは,毎秒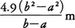 である。bがaに非常に近い場合は,この短い時間内では物体の速さは上の平均の速さにほぼ等しいと考えてもよいが,厳密にいうと,この短い時間内でも速さは時々刻々変化している。例えば,落下し始めてから1秒後の近くのようすを考えてみると,1秒後からb秒後までの平均の速さは(単位を省略して書くと),
である。bがaに非常に近い場合は,この短い時間内では物体の速さは上の平均の速さにほぼ等しいと考えてもよいが,厳密にいうと,この短い時間内でも速さは時々刻々変化している。例えば,落下し始めてから1秒後の近くのようすを考えてみると,1秒後からb秒後までの平均の速さは(単位を省略して書くと),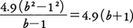 であるから,1秒後の瞬間の状態を調べるため,bを限りなく1に近づけると,上の式の値は4.9(1+1),すなわち9.8に限りなく近づく。こうして求められた毎秒9.8mという速さは,落下し始めてから1秒後の瞬間の速さと考えることができる。
であるから,1秒後の瞬間の状態を調べるため,bを限りなく1に近づけると,上の式の値は4.9(1+1),すなわち9.8に限りなく近づく。こうして求められた毎秒9.8mという速さは,落下し始めてから1秒後の瞬間の速さと考えることができる。
以上の考え方を一般の関数y=f(x)にあてはめてみよう。変数xの値がaからbまで変化するときに,関数の値はf(a)からf(b)までf(b)-f(a)だけ変化するから,このときのxの値の変化⊿x=b-aに対する関数の値yの変化⊿y=f(b)-f(a)の割合は,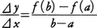 である。これは前の例における平均の速さに当たるもので,この値を,xがaからbまで変化するときの関数f(x)の平均変化率という。次に,前の例の瞬間の速さに当たるものとして,x=aにおける変化率を考えるため,bをaに近づけてみる。bがaに限りなく近づくとき上の平均変化率が一定の値に限りなく近づく場合,すなわち有限な極限値,
である。これは前の例における平均の速さに当たるもので,この値を,xがaからbまで変化するときの関数f(x)の平均変化率という。次に,前の例の瞬間の速さに当たるものとして,x=aにおける変化率を考えるため,bをaに近づけてみる。bがaに限りなく近づくとき上の平均変化率が一定の値に限りなく近づく場合,すなわち有限な極限値,
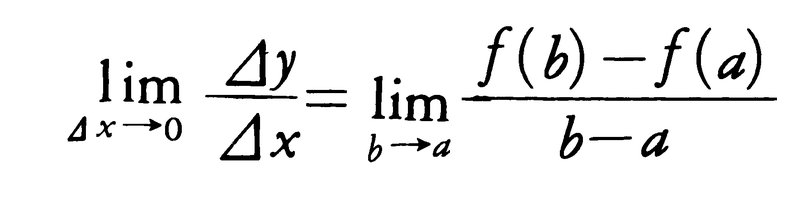
が存在する場合に,この値を\(\frac{dy}{dx}\),またはf′(a)で表し,関数f(x)のx=aにおける変化率,または微分係数という。f′(a)が存在するとき,関数fはaにおいて微分可能,または微分できるという。
微分係数には次のような幾何学的解釈を与えることができる。xy平面上にy=f(x)のグラフを描くと,x=aからx=bまでの平均変化率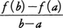 は,グラフの上の2点A(a,f(a)),B(b,f(b))を結ぶ直線ABの傾きを表している(図1)。bをaに近づけると,点Bはグラフ上を動きながら点Aに近づく。このとき直線ABの傾き,すなわち上記の平均変化率の値は,f′(a)に近づく。したがって直線ABは,点Aを通って傾きがf′(a)である直線ATに限りなく近づく。直線ATはグラフ上の点Aにおけるこのグラフの接線である。よって,微分係数f′(a)はy=f(x)のグラフ上の点A(a,f(a))における接線の傾きを表し,したがってその接線の方程式は,
は,グラフの上の2点A(a,f(a)),B(b,f(b))を結ぶ直線ABの傾きを表している(図1)。bをaに近づけると,点Bはグラフ上を動きながら点Aに近づく。このとき直線ABの傾き,すなわち上記の平均変化率の値は,f′(a)に近づく。したがって直線ABは,点Aを通って傾きがf′(a)である直線ATに限りなく近づく。直線ATはグラフ上の点Aにおけるこのグラフの接線である。よって,微分係数f′(a)はy=f(x)のグラフ上の点A(a,f(a))における接線の傾きを表し,したがってその接線の方程式は,
y-f(a)=f′(a)(x-a)
と表される(図2)。
関数y=f(x)がある区間のすべての点で微分可能なとき,その区間の点xにおける微分係数をf′(x)と書けば,f′(x)はまたxの関数と考えることができる。この関数を初めの関数y=f(x)の導関数といい,記号\(\frac{dy}{dx}\),f′(x)のほかに,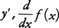 などでも表す。関数f(x)の導関数を求めることを,関数f(x)を微分するという。
などでも表す。関数f(x)の導関数を求めることを,関数f(x)を微分するという。
関数f(x)がx=aで微分可能ならばその点で連続であるが,逆は一般に成立しない。例えばf(x)=|x|(xの絶対値)はx=0において連続であるがf′(0)は存在しない。K.ワイヤーシュトラスは,ある区間で連続であって,その区間のすべての点で微分可能でない関数の例を具体的に与え,当時の学界の注目を引いた。
関数f(x)の導関数f′(x)がまた微分係数をもつとき,これをfの第二次微分係数といい,xにおけるfの第二次微分係数をxの関数と考えたものを,関数y=f(x)の第二次導関数といって,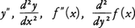 などで表す。このようにして順々に第n次微分係数,第n次導関数を定義し,
などで表す。このようにして順々に第n次微分係数,第n次導関数を定義し,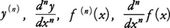 などで表す。
などで表す。
微分法
ここでは導関数を求める具体的演算としての微分法について述べる。
関数f,gが微分可能ならば,その一次結合af+bg(a,bは定数),積f・gは微分可能であり,またg≠0なる点では商f/gも微分可能であって,次の各式が成立する。
(af+bg)′=af′+bg′ ……(1)
(f・g)′=f′・g+f・g′ ……(2)
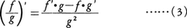
また,f(x)=c(定数)ならばf′(x)≡0であり,f(x)=xならばf′(x)≡1である。このことと(2)とから数学的帰納法により,すべての整数n≧0に対して,
(xn)′=nxn⁻1 ……(4)
となることが証明される。ただしn=0のときは,(4)の右辺はx=0のときも含めて恒等的に0と見なすものとする。(4)と(1)とから,任意の整関数(整式で表される関数)は微分可能であって,その導関数もまた整関数であることがわかり,このことと(3)とから,有理関数はその分母が0でない点においては微分可能であって,その導関数もまた有理関数であることがわかる。なお,整数n≧0に対して(4)が成り立つことと(3)とから,すべての整数nに対して(4)が成り立つことがわかる。(1)を繰り返すと,
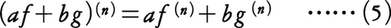
(2)を繰り返すと,
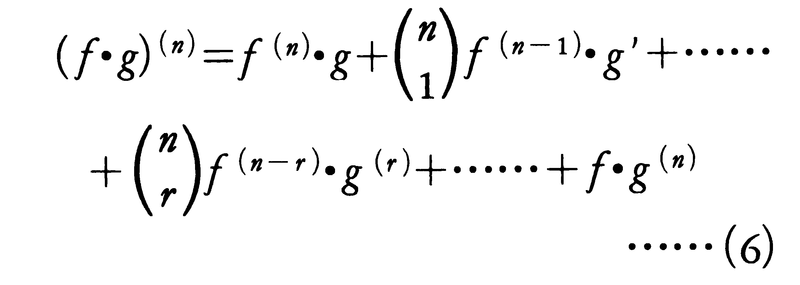
ただし,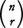 は二項係数であってnCr(組合せの数)とも書く。すなわち,
は二項係数であってnCr(組合せの数)とも書く。すなわち,
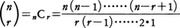
(6)をライプニッツの公式という。
合成関数の微分法
y=f(x)がx=aにおいて微分可能であり,z=g(y)がb=f(a)において微分可能であれば,xがaに十分近いときfの連続性によりyはbに近い値をとるから,aのある近傍で合成関数z=φ(x)=g(f(x))が定義される。この関数はx=aで微分可能であってφ′(a)=g′(b)f′(a)が成り立つ。これは,

とも書ける。(7)を繰り返して,y=f(x),z=g(y),w=h(z)なるとき,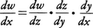 などが得られる。
などが得られる。
逆関数の微分法
y=f(x)がある区間で単調な関数であって微分可能であり,導関数f′(x)がその区間で0にならないならば,f(x)の逆関数x=φ(y)もまたすべての点で微分可能であってφ′(y)=1/f′(φ(y))が成り立つ。すなわち,逆関数の導関数\(\frac{dx}{dy}\)は,

によって計算される。例えばy=x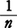 (x>0)はx=ynの逆関数であるから,(8)により,
(x>0)はx=ynの逆関数であるから,(8)により,
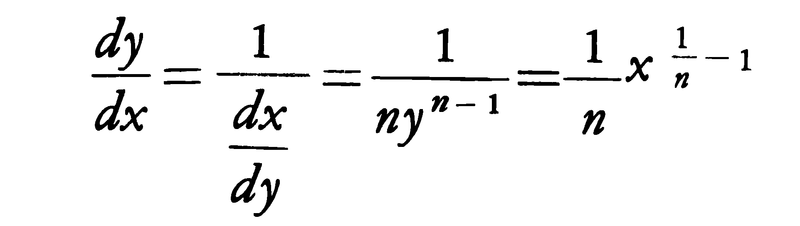
これと合成関数の微分法(7)によって,
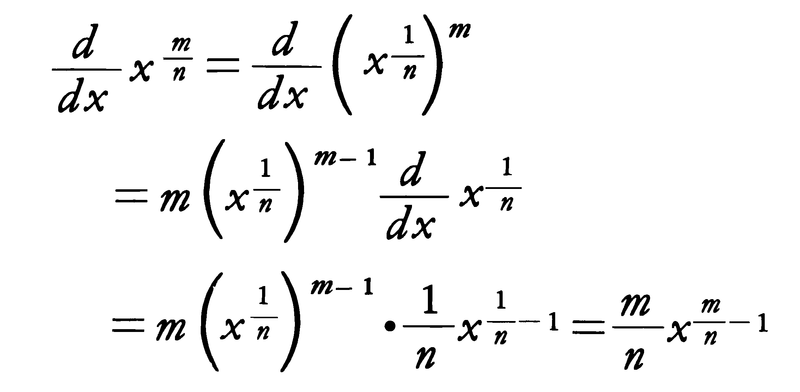
となる。すなわち,任意の有理数αに対して公式,
(xα)′=αxα⁻1 (x>0) ……(9)
が成り立つ。
媒介変数で表された関数の微分法
xとyの関係が媒介変数tによって,x=f(t),y=g(t)と与えられているとき,x=f(t)からtをxの関数と考えてt=φ(x)とし,これをy=g(t)に代入するとy=g(φ(x))となってyはxの関数になる。したがって合成関数,逆関数の微分法により,
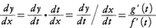
となり,\(\frac{dy}{dx}\)がf,gから計算される。
次の結果も公式として用いられる(逆三角関数は主値を表す)。
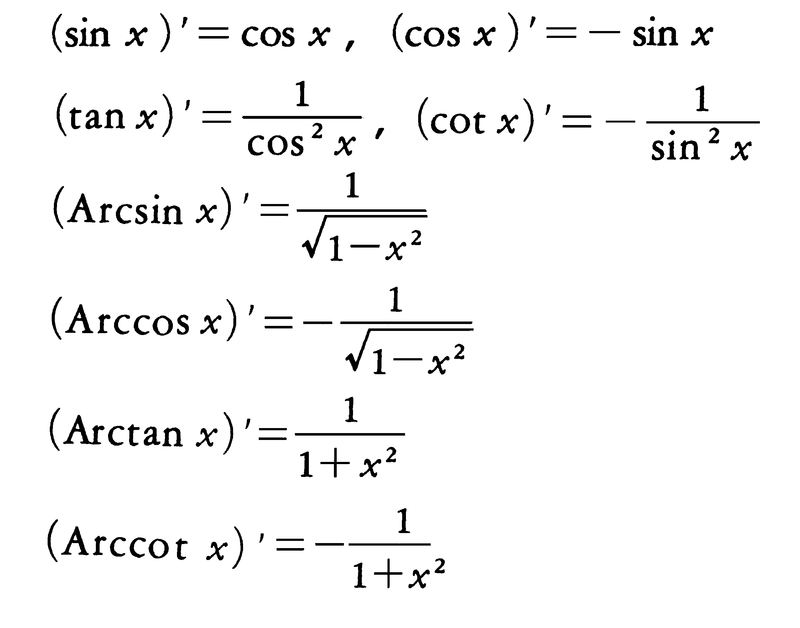
aを1に等しくない正の定数とするとき,
(ax)′=axloga,とくに(ex)′=ex
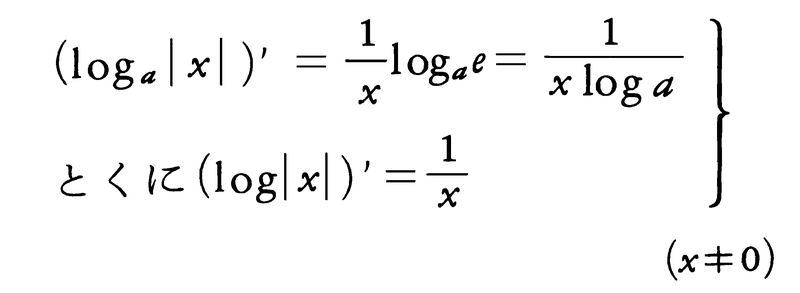
最後の公式を用いると,(9)が任意の実数αに対して成り立つことが次のようにしてわかる。y=xα(x>0)として両辺の自然対数をとるとlogy=αlogx,この両辺をxについて微分すると,上の最後の公式と(7)により,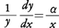
すなわち,
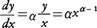
となり,任意の実数αに対して(9)が示された。一般に,y=f(x)の両辺の対数をとって上のようにしてy′を計算することを対数微分法という。
速度と加速度
変化率の説明で例にあげた落下する物体の〈瞬間の速さ〉の考え方で,一般の運動についての速度が定義される。
数直線上を運動する点Pの時刻tにおける位置を,その座標xで表すと,xはtの関数としてx=f(t)の形に表される。このとき\(\frac{dx}{dt}\),すなわちf′(t)を,時刻tにおける点Pの速度といい,速度の絶対値|\(\frac{dx}{dt}\)|を時刻tにおける点Pの速さ,または速度の大きさという。速度v=f′(t)もまた時刻tの関数である。vのtに関する変化率αを加速度という。すなわち,
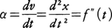
また|α|を加速度の大きさという。
次に,平面上を運動する点Pの座標(x,y)が時刻tの関数としてx=f(t),y=g(t)で与えられているとする。点Pからx軸,y軸に下ろした垂線をそれぞれPA,PBとすると,Pの運動によってA,Bはそれぞれx軸,y軸上を運動し,時刻tにおいて,
Aの位置はx=f(t),
速度は\(\frac{dx}{dt}\)=f′(t)
Bの位置はy=g(t),
速度は\(\frac{dy}{dt}\)=g′(t)
となる。このとき\(\frac{dx}{dt}\),\(\frac{dy}{dt}\)を成分とするベクトル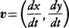 を時刻tにおける点Pの速度という。また,
を時刻tにおける点Pの速度という。また,
vx=\(\frac{dx}{dt}\),vy=\(\frac{dy}{dt}\)
をそれぞれ速度のx成分,y成分といい,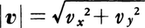 を速さ,または速度の大きさという。次に,時刻tにおけるA,Bの加速度はそれぞれ,
を速さ,または速度の大きさという。次に,時刻tにおけるA,Bの加速度はそれぞれ,
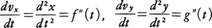
である。これらを成分とするベクトル
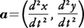
を加速度という。
ax=\(\frac{d^2x}{dt^2}\),ay=\(\frac{d^2y}{dt^2}\)
をそれぞれ加速度のx成分,y成分といい,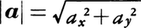 を加速度の大きさという。
を加速度の大きさという。
空間を運動する点Pの速度,加速度についても,その座標x,y,zの速度,加速度を用いて上と同様に定義される。
平均値の定理,テーラーの公式
関数のグラフを見て考えると,すべての点でf′(x)>0となる関数f(x)は単調増加であることが予想されるが,このような直観的考察は厳密な証明ではない。一般に関数f(x)の増減の状態をその微分係数を用いて調べるとき,次の平均値の定理が重要である。
f(x)が閉区間[a,b]で連続,かつ開区間(a,b)で微分可能ならば,
f(b)-f(a)=(b-a)f′(ξ) ……(10)
となるξが開区間(a,b)の中に存在する。
この定理でf(a)=f(b)という特別な場合はロルRolleの定理と呼ばれる。平均値の定理の証明はロルの定理に帰着され,ロルの定理は,有限閉区間で連続な関数はその区間で最大値,最小値をとる,という定理を用いて証明される。平均値の定理は幾何学的には,y=f(x)のグラフの上の2点A(a,f(a))とB(b,f(b))とを結ぶ直線に平行な接線が引けるような点Cが,グラフ上でAとBとの間にあることを意味する(図3)。平均値の定理においてb-a=h,(ξ-a)/h=θとおくと,この定理は,
f(a+h)=f(a)+hf′(a+θh) (0<θ<1)
なるθがあるという形に述べられる。この式はh<0でも成り立つ。
平均値の定理を用いて次のことが証明される。ある区間でf′(x)≧0ならばf(x)はその区間で単調増加である。とくに,その区間でつねにf′(x)>0ならばf(x)は狭義単調増加である。また,ある区間でf′(x)≦0ならばf(x)はその区間で単調減少である。とくにその区間でつねにf′(x)<0ならば,f(x)は狭義単調減少である。上のことから,ある区間でいたるところf′(x)=0ならば,f(x)はその区間で定数になる。したがってまた,ある区間で導関数の等しい二つの関数の差はその区間で定数である。
微分係数は関数の極大,極小を求めるのに用いられる。x=aにおいて関数fが極大であるとは,aのある近傍でfが定義されていて,かつその近傍の中のすべてのxに対してf(x)≦f(a)が成り立つことである。そのときf(a)を極大値という。不等号≦を≧で置き換えることにより,極小,極小値の定義が得られる。f(x)がx=aで極大,または極小であってf′(a)が存在すればf′(a)=0である。だから,微分可能な関数fの極大値,極小値を求めるのには,方程式f′(x)=0を解きその解aの前後におけるf′(x)の符号の変化を調べる。すなわち,x<aの側からx>aの側に移るときf′(x)の符号が正から負に変わればf(a)は極大値であり,負から正に変わればf(a)は極小値である。なお,f′(a)=0であってもf(a)は極大,または極小であるとは限らない。例えばf(x)=x3についてはf′(0)=0であるがy=f(x)のグラフは図4のようになり,f(0)は極大でも極小でもない。
次の定理は平均値の定理の一般化で,コーシーの平均値の定理と呼ばれている。f(x),g(x)が閉区間[a,b]で連続,開区間(a,b)で微分可能でg′(x)≠0ならば,
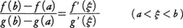
を満たすξが存在する。この事実は極限の計算に利用される。例えば,f,gがaの近傍で微分可能であってf(a)=g(a)=0であり,f′(x)/g′(x)がaで連続ならば,
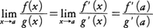
すなわち,f(a)/g(a)が0/0の形になるときには,上の極限値の計算は,分母,分子を別々に微分してx→aの極限値を計算すればよい。これをロピタルの定理という。例えば,
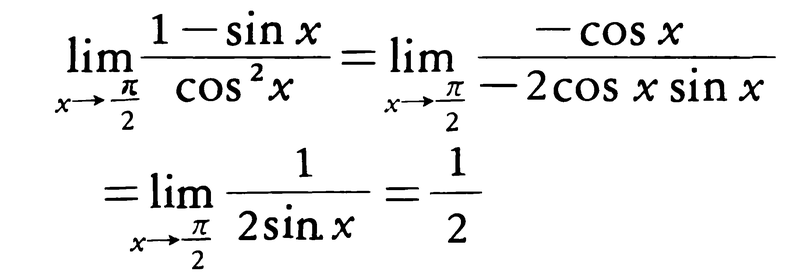
f(x)が開区間Iでn回微分可能のとき,Iの中の点aを固定して,Iの任意の点xに対して,
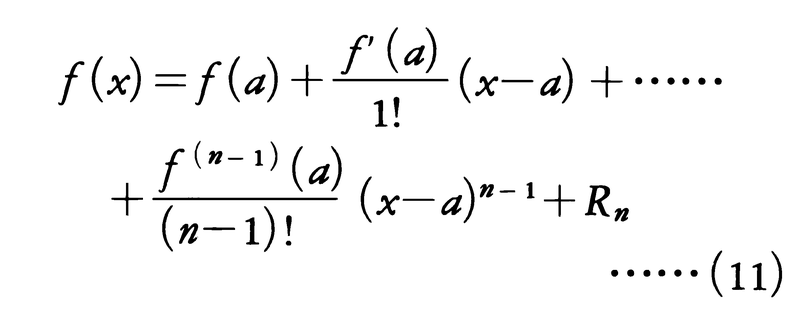
とおくと,
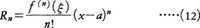
となるようなξがaとxとの間にある。これをテーラーの公式といい,Rnをn次の剰余項という。f⁽n⁾(x)がx=aで連続ならば,
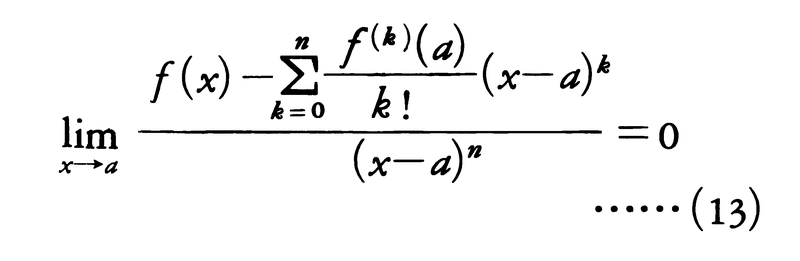
が成り立つから,xがaに近い値をとるときf(x)の値の近似値としてn次の整式,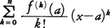 の値を用いることができる。これをxがaに近いときのf(x)の第n近似式という。|Rn+1|はその誤差である。式(12)はこの誤差の評価に用いられる。また,aのある近傍で一様に,
の値を用いることができる。これをxがaに近いときのf(x)の第n近似式という。|Rn+1|はその誤差である。式(12)はこの誤差の評価に用いられる。また,aのある近傍で一様に,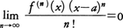 となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
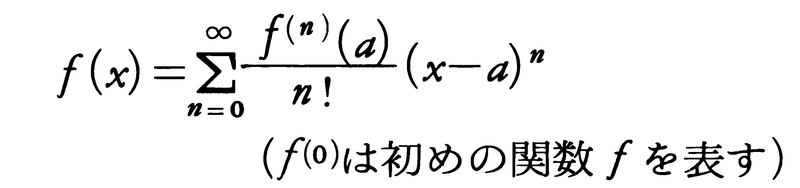
が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数をテーラー級数という。
微分
関数y=f(x)がx=aにおいて微分可能ならば,xのaからの変化⊿x→0のとき\(\frac{⊿y}{⊿x}\)→f′(a)であるから,
\(\frac{⊿y}{⊿x}\)-f′(a)=ε
とおけば,
⊿y=f′(a)⊿x+ε・⊿x ……(14)
⊿x→0のときε→0 ……(15)
となる。だから,(14)において⊿x→0とするとき(15)によりε・⊿xは⊿xよりも速く0に近づくことになり,(14)の右辺は第1項が主要な部分であるから,これを〈aにおける⊿xに対するyの微分〉と呼び,記号dyで表す。独立変数xの微分はdx=⊿xと定める。こうすると,
dy=f′(a)dx
となり,微分係数の記号\(\frac{dy}{dx}\)=f′(a)と対応する。
偏微分法
二つ以上の変数x,y,……の関数f(x,y,……)があるとき,これを一つの変数,例えばxだけに注目して,他の変数は固定して定数と考え,xの関数と考えて微分することを,関数fをxについて偏微分するといい,それによって得られる微分係数を,変数xに関するfの偏微分係数と呼んで\(\frac{∂f}{∂x}\),またはfxと書く。簡単のために2変数の関数f(x,y)について書くと,
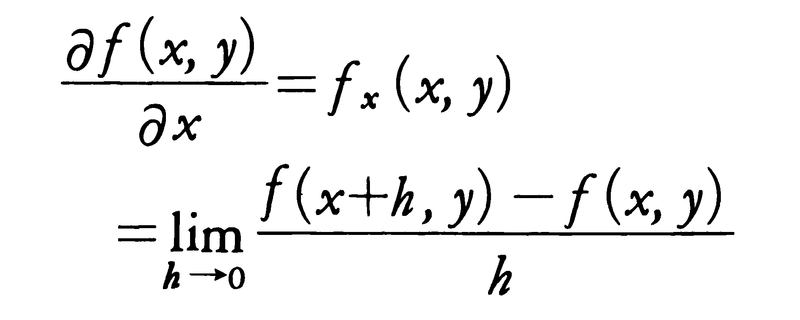
によってfのxに関する偏微分係数が定義される。この偏微分係数をx,yの関数と考えるとき,その関数をfのxに関する偏導関数という。偏微分係数,または偏導関数を求める手続きを偏微分法という。実際の計算には,前に述べた1変数の関数の微分法の公式が使われる。z=f(x,y)とおくとき,上に述べた偏導関数fx(x,y)を\(\frac{∂z}{∂x}\),またはzxとも書く。xを固定してyについて微分することにより変数yに関する偏微分係数,偏導関数を同様に定義し,
\(\frac{∂f}{∂y}\),fy,\(\frac{∂z}{∂y}\),zy
などで表す。\(\frac{∂f}{∂x}\)がまたx,yに関して偏微分できるときは,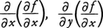 を考えることができる。これらをそれぞれ,
を考えることができる。これらをそれぞれ,
\(\frac{∂^2f}{∂x^2}\),\(\frac{∂^2f}{∂y∂x}\)
で表す。\(\frac{∂^2f}{∂x^2}\)をfxx,\(\frac{∂^2z}{∂x^2}\),zxxなどとも書き,\(\frac{∂^2f}{∂y∂x}\)をfxy,\(\frac{∂^2z}{∂y∂x}\),zxyなどとも書く。\(\frac{∂f}{∂y}\)がx,yについて偏微分できるときは,上と同様にして,
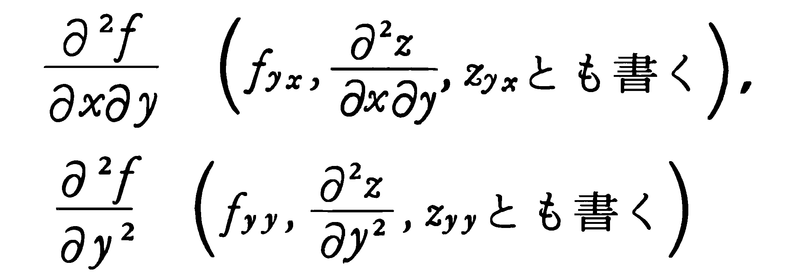
が定義される。これらをz=f(x,y)の2階偏導関数という。同様の考えを繰り返して,高階の偏導関数も帰納的に定義される。fxyとfyxとは偏微分する順序が異なるので一般には相等しいとは限らないが,例えばfxyとfyxがともに連続なら,fxy=fyxとなることが知られている。z=f(x,y)をxyz空間における曲面と見なすとき,その曲面上の1点(a,b,c)(c=f(a,b))における接平面の方程式は,
z-c=fx(a,b)(x-a)+fy(a,b)(y-b)
で与えられる。fx(a,b),fy(a,b)はそれぞれ接平面のx方向,y方向の傾きである。このことから,f(x,y)が点(a,b)で極値をとればfx(a,b)=fy(a,b)=0となることがわかるが,その逆は成立しない。
合成関数の偏微分法
zがx,yの関数,すなわちz=f(x,y)で表され,x,yがいずれもu,vの関数でそれぞれx=φ(u,v),y=ψ(u,v)と表されるならば,このx,yの式をfに代入することによりzはu,vの関数になる。このzをu,vで偏微分する公式は,次のように与えられる。
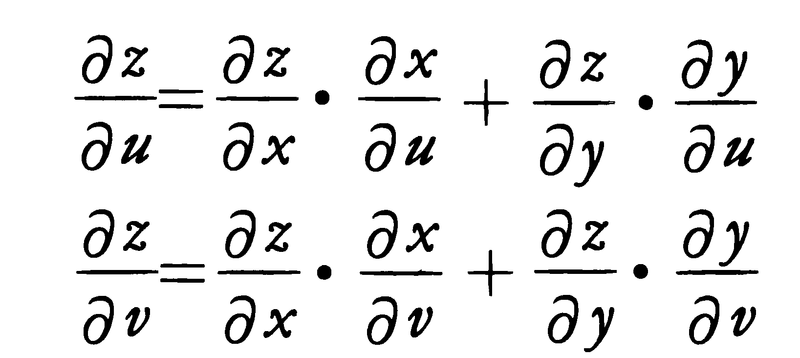
とくにx,yが一つの変数tの関数x=φ(t),y=ψ(t)ならば,zは1変数tの関数である。このときzをtで微分する公式は,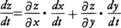 で与えられる。
で与えられる。
全微分
関数z=f(x,y)の定義域の中に1点(a,b)をとり,そこから変数をそれぞれ⊿x,⊿yだけ変化させたとき,点(a,b)と点(a+⊿x,b+⊿y)との距離ρは,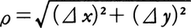 であり,そのとき関数の値zの変化は,
であり,そのとき関数の値zの変化は,
⊿z=f(a+⊿x,b+⊿y)-f(a,b)
である。fx,fyがともに連続ならば,
⊿z=fx(a,b)⊿x+fy(a,b)⊿y+ε(⊿x,⊿y)・ρ ……(16)
とおくと,ρ→0のときε(⊿x,⊿y)→0となる。したがってε(⊿x,⊿y)・ρはρよりも速く0に近づく量であり,(16)の右辺の主要部は,
fx(a,b)⊿x+fy(a,b)⊿y
である。これを(a,b)におけるzの全微分といいdzで表す。独立変数x,yの全微分はdx=⊿x,dy=⊿yと定める。したがってzの全微分は,
dz=fx(a,b)dx+fy(a,b)dy
となる。これに対してfx(a,b)dx,fy(a,b)dyを偏微分という。偏微分法のことを単に偏微分と呼ぶのは略称であるが,一般に通用しているので,本事典の項目名でも偏微分法とすべきところを利用者の便宜のため偏微分としてある。なお,偏導関数のことを偏微分と呼ぶのは,正しい用語ではない。
2変数の関数の偏微分法に関して以上に述べたことは,一般の多変数の関数の場合もまったく同様に考えることができる。例えば3変数の関数f(x,y,z)の偏導関数\(\frac{∂f}{∂x}\)は,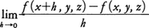 によって定義される。また合成関数の偏微分法の公式として,zがm変数y1,y2,……,ymの関数z=f(y1,y2,……,ym)であって,各yiがn変数x1,x2,……,xnの関数,
によって定義される。また合成関数の偏微分法の公式として,zがm変数y1,y2,……,ymの関数z=f(y1,y2,……,ym)であって,各yiがn変数x1,x2,……,xnの関数,
yi=gi(x1,x2,……,xn) (i=1,2,……,m)
ならば,zはx1,x2,……,xnの関数と考えられるが,このとき公式,
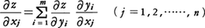
が成立するのである。
→微積分学
執筆者:伊藤 清三


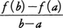 である。これらの値を調べるだけでも関数f(x)のだいたいのようすはわかるが,もっとくわしくf(x)の状態を知るためには,例えばx=aのときの〈瞬間的変化〉の状態を調べる必要が起こる。この瞬間的な変化の考えを数学的に厳密に定式化すると,すぐ後に説明するところの微分係数,導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。微分法のことを単に微分ということが多いが,これは〈微分することdifferentiation〉からきた略称である。本項では,微分法の具体的計算法やそのための公式,導関数のおもな性質やその応用について述べるので,項目名は微分法とすべきであろうが,微分の略称が一般に広く使われているのでこの略称を項目名とした。数学用語としての微分の本来の意味は,この項目中で後ほど〈微分〉という
である。これらの値を調べるだけでも関数f(x)のだいたいのようすはわかるが,もっとくわしくf(x)の状態を知るためには,例えばx=aのときの〈瞬間的変化〉の状態を調べる必要が起こる。この瞬間的な変化の考えを数学的に厳密に定式化すると,すぐ後に説明するところの微分係数,導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。微分法のことを単に微分ということが多いが,これは〈微分することdifferentiation〉からきた略称である。本項では,微分法の具体的計算法やそのための公式,導関数のおもな性質やその応用について述べるので,項目名は微分法とすべきであろうが,微分の略称が一般に広く使われているのでこの略称を項目名とした。数学用語としての微分の本来の意味は,この項目中で後ほど〈微分〉という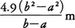 である。bがaに非常に近い場合は,この短い時間内では物体の速さは上の平均の速さにほぼ等しいと考えてもよいが,厳密にいうと,この短い時間内でも速さは時々刻々変化している。例えば,落下し始めてから1秒後の近くのようすを考えてみると,1秒後からb秒後までの平均の速さは(単位を省略して書くと),
である。bがaに非常に近い場合は,この短い時間内では物体の速さは上の平均の速さにほぼ等しいと考えてもよいが,厳密にいうと,この短い時間内でも速さは時々刻々変化している。例えば,落下し始めてから1秒後の近くのようすを考えてみると,1秒後からb秒後までの平均の速さは(単位を省略して書くと),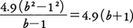 であるから,1秒後の瞬間の状態を調べるため,bを限りなく1に近づけると,上の式の値は4.9(1+1),すなわち9.8に限りなく近づく。こうして求められた毎秒9.8mという速さは,落下し始めてから1秒後の瞬間の速さと考えることができる。
であるから,1秒後の瞬間の状態を調べるため,bを限りなく1に近づけると,上の式の値は4.9(1+1),すなわち9.8に限りなく近づく。こうして求められた毎秒9.8mという速さは,落下し始めてから1秒後の瞬間の速さと考えることができる。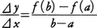 である。これは前の例における平均の速さに当たるもので,この値を,xがaからbまで変化するときの関数f(x)の
である。これは前の例における平均の速さに当たるもので,この値を,xがaからbまで変化するときの関数f(x)の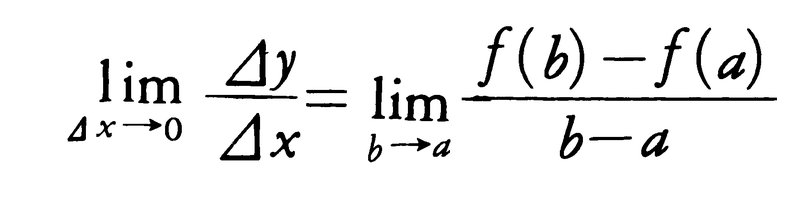
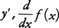 などでも表す。関数f(x)の導関数を求めることを,関数f(x)を微分するという。
などでも表す。関数f(x)の導関数を求めることを,関数f(x)を微分するという。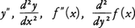 などで表す。このようにして順々に第n次微分係数,第n次導関数を定義し,
などで表す。このようにして順々に第n次微分係数,第n次導関数を定義し,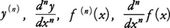 などで表す。
などで表す。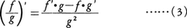
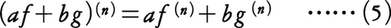
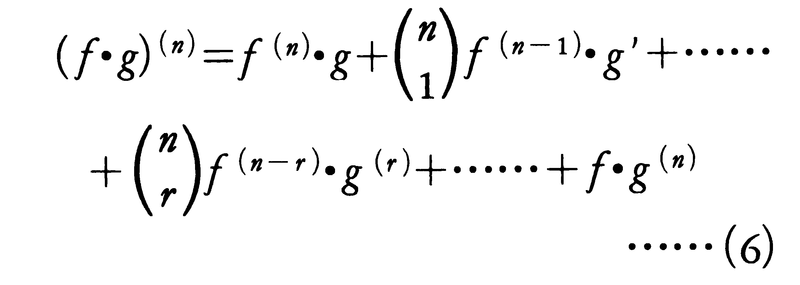
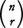 は二項係数であってnCr(組合せの数)とも書く。すなわち,
は二項係数であってnCr(組合せの数)とも書く。すなわち,

 などが得られる。
などが得られる。
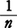 (x>0)はx=ynの逆関数であるから,(8)により,
(x>0)はx=ynの逆関数であるから,(8)により,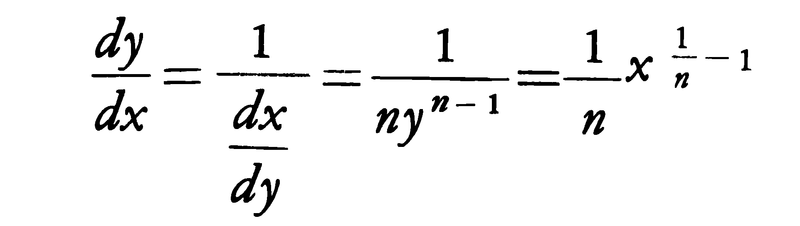
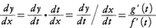
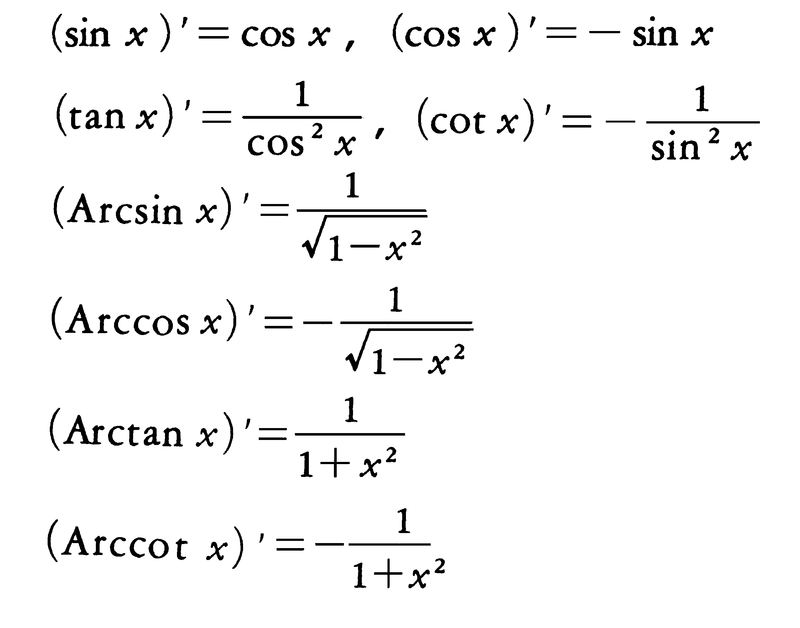
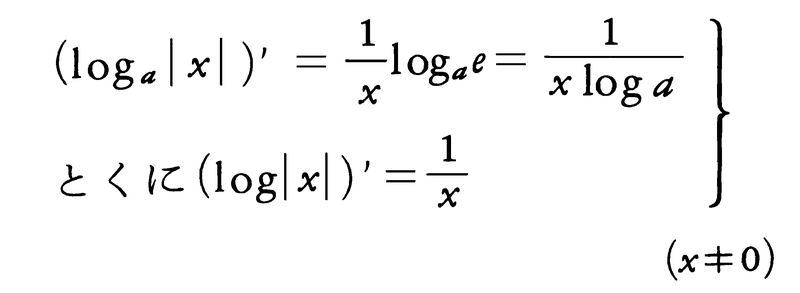
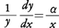
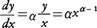
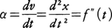
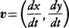 を時刻tにおける点Pの速度という。また,
を時刻tにおける点Pの速度という。また,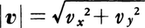 を速さ,または速度の大きさという。次に,時刻tにおけるA,Bの加速度はそれぞれ,
を速さ,または速度の大きさという。次に,時刻tにおけるA,Bの加速度はそれぞれ,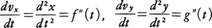
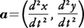
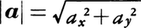 を加速度の大きさという。
を加速度の大きさという。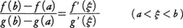
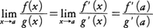
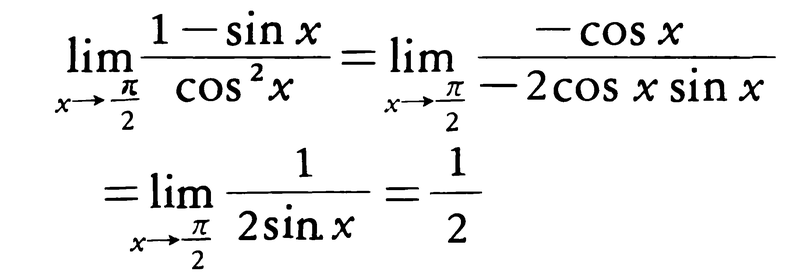
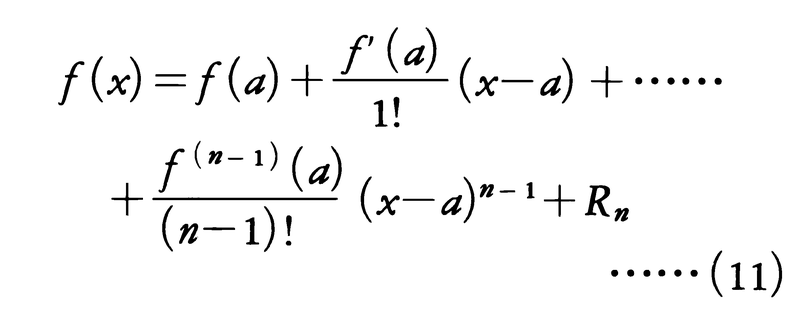
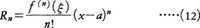
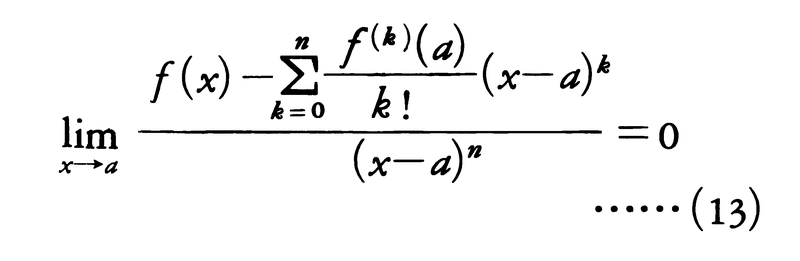
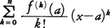 の値を用いることができる。これをxがaに近いときのf(x)の第n近似式という。|Rn+1|はその誤差である。式(12)はこの誤差の評価に用いられる。また,aのある近傍で一様に,
の値を用いることができる。これをxがaに近いときのf(x)の第n近似式という。|Rn+1|はその誤差である。式(12)はこの誤差の評価に用いられる。また,aのある近傍で一様に,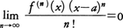 となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,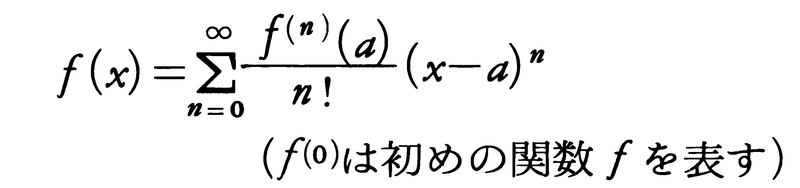
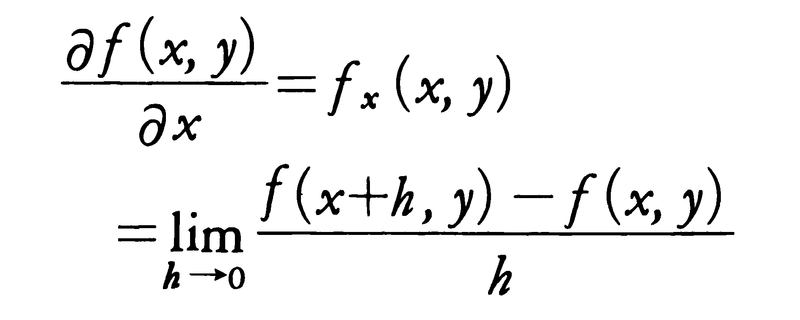
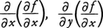 を考えることができる。これらをそれぞれ,
を考えることができる。これらをそれぞれ,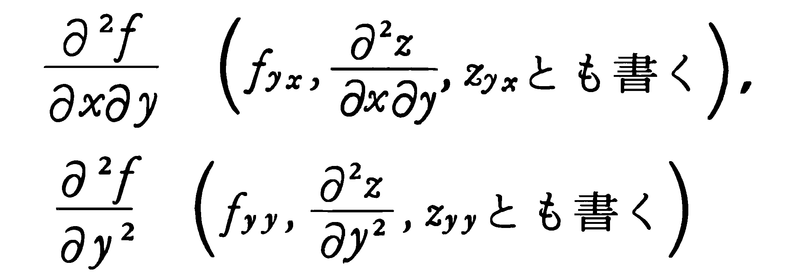
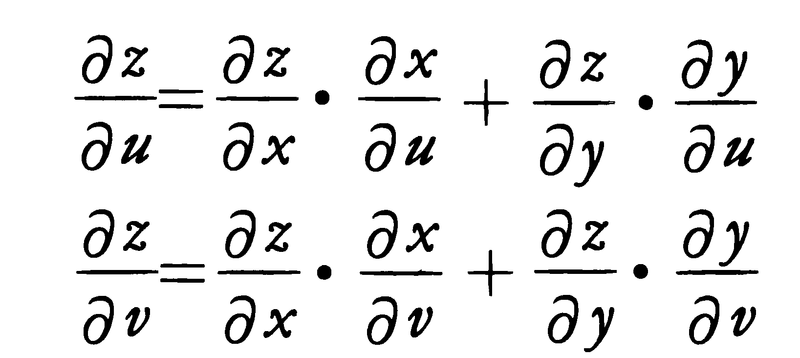
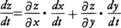 で与えられる。
で与えられる。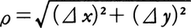 であり,そのとき関数の値zの変化は,
であり,そのとき関数の値zの変化は,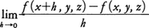 によって定義される。また合成関数の偏微分法の公式として,zがm変数y1,y2,……,ymの関数z=f(y1,y2,……,ym)であって,各yiがn変数x1,x2,……,xnの関数,
によって定義される。また合成関数の偏微分法の公式として,zがm変数y1,y2,……,ymの関数z=f(y1,y2,……,ym)であって,各yiがn変数x1,x2,……,xnの関数,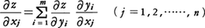
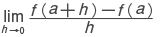 が存在するとき,y=f(x)は x=a において微分可能といい,この極限値を f'(a)と表して,x=a における微分係数という。微分係数 f'(a)は,関数 y=f(x)の x=a における局所的な変化率を表す。微分係数を x の関数とみなしたものを f'(x)と表し,
が存在するとき,y=f(x)は x=a において微分可能といい,この極限値を f'(a)と表して,x=a における微分係数という。微分係数 f'(a)は,関数 y=f(x)の x=a における局所的な変化率を表す。微分係数を x の関数とみなしたものを f'(x)と表し,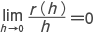 となり,h に対して f'(x)h を対応させる写像は,関数の増分の 1次式による最もよい近似であると考えられる。一般に,微分は関数を局所的に 1次式によって近似する操作である。2変数関数の微分は,
となり,h に対して f'(x)h を対応させる写像は,関数の増分の 1次式による最もよい近似であると考えられる。一般に,微分は関数を局所的に 1次式によって近似する操作である。2変数関数の微分は,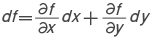 で与えられる。
で与えられる。