改訂新版 世界大百科事典 「確率制御」の意味・わかりやすい解説
確率制御 (かくりつせいぎょ)
stochastic control
確率微分方程式に従って運動する系に対する制御理論。B（t）をn次元ブラウン運動とする。与えられた領域Γ（制御域という）の値をとる確率過程U（t）は，過去の部分（U（θ），B（θ），θ≦t）がブラウン運動の増分B（s）－B（t）とは独立のとき，許容されるコントロールと呼ばれる。U（t）を用いた場合の運動は確率微分方程式dX（t）＝α（X（t），U（t））dB（t）＋γ（X（t），U（t））dtで与えられる。α，γが有界で滑らかなとき，初期値X（0）＝xが与えられると，解X（t）が定まる。評価関数，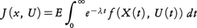
を最大（あるいは最小）にするように許容されるコントロールを選ぶのが確率制御である。
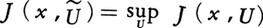（価関数という）となるŨを最適制御と呼ぶ。価関数は適当な条件の下でベルマン方程式，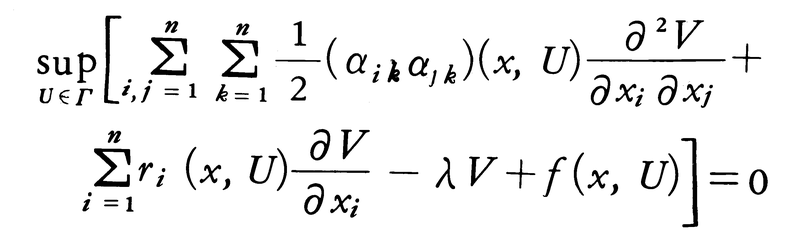
を満たし，左辺の最大値を与えるŨ（x）により最適制御を求めることができる。
執筆者：西尾 真喜子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 