確率微分方程式（読み）カクリツビブンホウテイシキ（その他表記）stochastic differential equation

デジタル大辞泉

かくりつ‐びぶんほうていしき〔‐ビブンハウテイシキ〕【確率微分方程式】

時間の経過とともにランダムに変動する量（確率過程）を扱う微分方程式。ブラウン運動における粒子の運動の記述、金融工学分野の株価やデリバティブの価格付けなどに用いられる。

出典　小学館

改訂新版　世界大百科事典

確率微分方程式 (かくりつびぶんほうていしき)
stochastic differential equation

ランダムな外力を伴う運動方程式。ブラウン運動を変換して，マルコフ過程を構成する問題から研究が始まり，伊藤清により確率論の一分野として確立された。雑音に汚染された自然現象の記述などに広く用いられる。n次元常微分方程式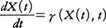，に従う運動に，ブラウン運動B（t）による摂動が加えられたとき，系の時間変化はdX（t）＝γ（X（t），t）dt＋α（X（t），t）dB（t）となり，確率微分方程式と呼ばれる。B（t）はtに関し微分不可能なため，正確にいえば，上記方程式は積分方程式，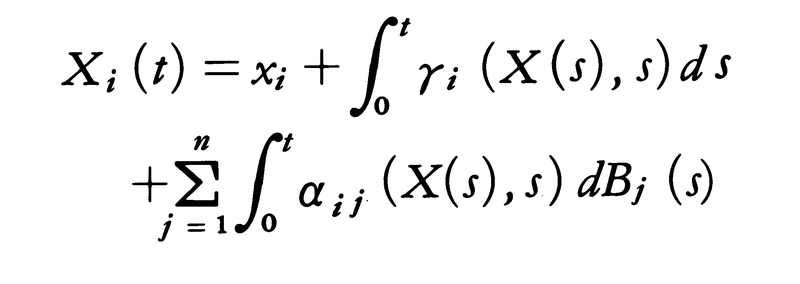

ただしB（t）＝（B₁（t），……，B_n（t）），X（t）＝（X₁（t），……，X_n（t））。第3項のdBによる積分は確率積分である。α，γが有界で，Xについてリプシッツ連続のとき方程式の解はただ一つ存在し，X（t）は初期値xと（B（θ），θ≦t）の関数になり，マルコフ過程を定める。α，γに関する条件を弱めても解は存在するが，一意性やマルコフ性にいろいろの問題が起こる。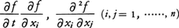がすべて有界連続関数となる有界なfに対し，X（t）が上記方程式の解であるとき，f（X（t），t）は次の確率微分方程式を満たす。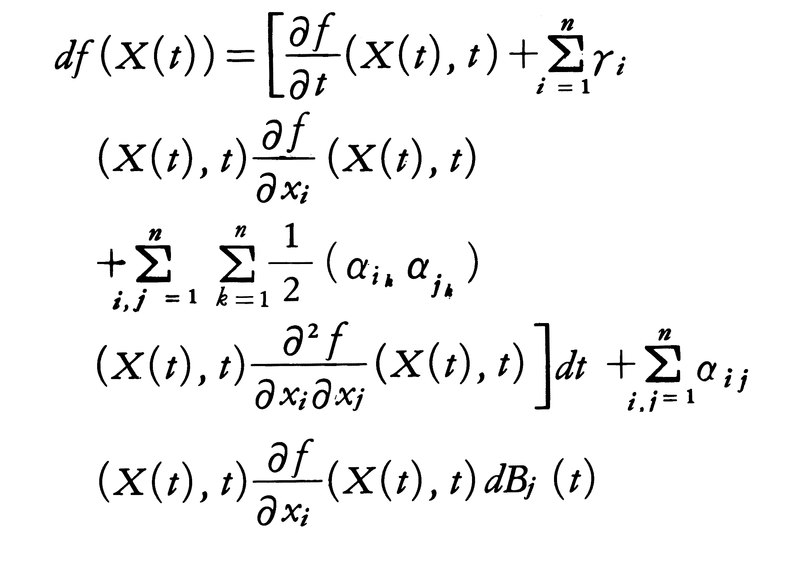

これはfを形式的にテーラー展開して，dB_i（t）dB_j（t）＝dt（i＝jのとき），dB_i（t）dB_j（t）＝0（i≠jのとき）として得られるが，伊藤公式と呼ばれ基本公式になっている。
執筆者：西尾 真喜子

出典　株式会社平凡社「改訂新版　世界大百科事典」