日本大百科全書(ニッポニカ) 「制御理論」の意味・わかりやすい解説
制御理論
せいぎょりろん
制御工学についての理論全般をいう。電気回路理論や通信理論を母体に、ここ数十年間に目覚ましい発展を遂げ、自動制御の発達の原動力となっている。
制御理論は、通常、フィードバック制御理論と、状態空間に基づくシステム制御理論とに大別される。前者は自動制御の発生時点からの中心課題であり、今日実用されているほとんどの制御装置の産みの親である。後者はシステムの複雑、高度化に対応する近代的な制御理論である。
[立花康夫]
フィードバック制御理論
線形制御
フィードバック制御理論の中心的課題は線形系に対し、入出力の因果関係をシステムの表現に用いる点が特徴である。線形系の入出力信号は有限階数の線形微分方程式により結び付けられている。この際入出力信号のラプラス変換をU(S)とY(S)とすれば、これらは
Y(S)=G(S)・U(S) (1)
という関係で表される。この際G(S)を伝達関数とよぶ。また、とくに入力としてインパルスやステップ信号を加えたときの出力信号の形状も系の特性を表していて、それぞれインパルス応答、ステップ応答という。
また入力に角周波数ωの単振動を加えた際の応答を周波数応答といいG(jω)で表される。ここで、
G(jω)=|G(jω)|ei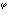
としたとき|G|はゲイン、 は位相角という。これら系を表す特性式を求めることを同定という。
は位相角という。これら系を表す特性式を求めることを同定という。
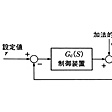
フィードバック制御では対象の出力を被制御量とよび、これを所定の設定値にするように制御系をのように組み込む。対象系の入出力に加わる種々の外乱により被制御量とその設定値の間には偏差が生じ、これを打ち消すように制御系が働く。設定値を変化させそれへの追従性の良否を論ずるのがサーボ問題で、設定値は一定で外乱による偏差を抑えることを問題にするのがレギュレーター問題である。で設定値より対象系の出力までを閉ループ特性といい、Gc(S)を制御系の伝達関数とすると、
H(S)=G(S)/(1+Gc(S)G(S)) (2)
で与えられる。
閉ループにすると、制御系の作り方によっては、すこしの外乱などにより発振のような不安定現象を生じる。これを調べることが安定性判別である。H(S)はSの有理式となる。その分母を表すSの多項式をA(S)としたとき、
A(S)=Sn+αn-1Sn-1+……
+α1S+α0=0 (3)
を特性方程式という。この根を特性根といい、それがすべてS複素平面の左半面にあれば安定である。これをA(S)の係数のみにより判定できるのがラウス‐フルビッツRouth-Hurwitz法である。これは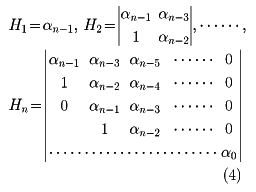
などの行列式がすべて正で、A(S)の係数がすべて正なら安定であることを保証している。
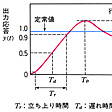
で設定値をステップ状に変化させた場合の被制御量の変化を閉ループステップ応答という。はその形状を示したものである。ここで立ち上り時間、遅れ時間および行き過ぎ時間は速応性の尺度を示し、行き過ぎ量は安定性の尺度を示し、整定時間は速応性および安定性の両方の評価尺度を示している。また整定値は設定値に一致すべきものであるが、制御系によってはこれらの値が異なる場合もあり、これを定常偏差という。これらの閉ループステップ応答の形状を指定してPID制御器(比例制御器proportional, integral and differential controller)を設計する方法としてニコルスZiegler Nicholsの方法やマーチンJ. Martinの方法などがあり、時間領域での設計法とよばれている。これに対して周波数領域からの設計法とよばれるものがある。特性根は応答特性と深く関連している。対象の周波数特性を複素平面上に描き、周波数ωを-∞から∞へと変化させたものをナイキストNyquist線図という。そして、ωを0~∞としたときのナイキスト軌跡が点-1+jを左側にみて描かれるならば、の系は安定となるというナイキストの安定判別法が成り立つ。利得|G(jω)|の対数20log10|G(jω)|および位相角 を縦軸とし、角周波数の対数を横軸とした図をボードBode線図という。は閉ループ特性のボード線図の例である。ゲインの最大値をピーク利得、ゲイン1のときの位相角をマイナス180度より計った値を位相余裕、位相角がマイナス180度のときの利得を利得余裕といい、これらの設定により所定の制御系を設計することができる。また20log|G|を縦軸にとり、
を縦軸とし、角周波数の対数を横軸とした図をボードBode線図という。は閉ループ特性のボード線図の例である。ゲインの最大値をピーク利得、ゲイン1のときの位相角をマイナス180度より計った値を位相余裕、位相角がマイナス180度のときの利得を利得余裕といい、これらの設定により所定の制御系を設計することができる。また20log|G|を縦軸にとり、 を横軸とし、閉ループ特性H(jω)のゲインMと位相角Nが一定となる曲線を描いたニコルス線図も周波数領域での設計に用いられる。
を横軸とし、閉ループ特性H(jω)のゲインMと位相角Nが一定となる曲線を描いたニコルス線図も周波数領域での設計に用いられる。
[立花康夫]
サンプル値制御
間欠的な信号を一部にもつ制御系をサンプル値制御系という。間欠信号はサンプラやコンピュータなどでつくられる。(1)は典型的なサンプル値制御系である。サンプラとは一定時間T(サンプル周期という)ごとに信号f(t)をf*(t)に変換する装置である。f*(t)は
で表され、サンプル周期T時間ごとの情報で表現される。ここでδ(t)はデルタ関数であり、サンプラの出力を制御対象に作用させる場合にはかならずその値にホールド素子を用いる。Tの間f(nT)の一定値を保持する0次保持がよく用いられる。サンプル値系ではアナログ系でのラプラス変換と同じようにZ変換が解析に用いられる。すなわち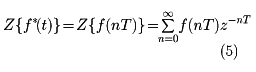
をZ変換とよぶ。(1)においてサンプル値制御器は、(2)のように数列f(kT)と数列y(kT)のみを扱うのでデジタル制御器ともいう。(3)の連続要素も入出力にサンプラを設けると、f*とy*の関係となる。(2)と(3)において、f*とy*または、f(kT)とy(kT)のZ変換をそれぞれF(z)とY(z)とすると、Y(z)/F(z)は系特有のzの式となる。たとえば(2)では
Y(z)=G(z)・F(z)
となる。このG(z)はパルス伝達関数とよばれる。パルス伝達関数でz=ejωTと置くと周波数特性が得られる。アナログ系と同じくインパルス応答およびステップ応答も用いられる。サンプル値系の安定性はz平面でパルス伝達関数の分母をなす特性多項式の根が単位円の内部にあることにより判定される。
サンプル値系も閉ループ特性を考えた時間領域での設計と周波数領域での設計法とがある。またデジタル制御系の特徴としてサンプル周期ごとの時刻のみでみると、有限時間で整定させることのできるデッドビートdeadbeat(有限整定応答)制御という方法も用いられている。
多くの場合制御する範囲では系を線形近似することができるが、リレー回路や飽和要素を含む系は非線形系としての扱いが必要で、記述関数法や位相解析法などが用いられる。
[立花康夫]
統計的制御
信号の不規則な変動を明確に記述して扱う統計的制御系の考えも用いられる。これは、アメリカのウィーナーにより大成された相関法を基にした最適フィルターの設計に基礎を置いている。
[立花康夫]
システム制御理論
システム制御理論では、系の入出力だけではなく、内部の構造までも明確に表現する立場をとる。また入出力も多変数を許す。入力をベクトルu=(u1,u2,……,um)Tで、出力をy=(y1,y2,……,yp)Tで表し、系の内部を表す状態変数をx=(x1,x2,……,xn)Tとすると、
x=Ax+Bu,x(t0)=x0 (6)
y=Cx+Du (7)
と表される。(6)は状態方程式、(7)を観測方程式とよぶ。システム制御理論はすべてこの二つの方程式を基にして展開される。
時刻t0で状態x0にあるとき、有限時間ののちに状態を原点Oにもたらす入力が存在する場合を可制御な状態といい、すべての状態が可制御のとき完全可制御という。また時刻t0で状態がx0のとき、t0より有限時間までの出力を観測してx0が定められる場合を可観測な状態といい、すべての状態が可観測のとき完全可観測という。これらの条件はすべて(6)と(7)の係数で表され、制御するうえでの系の構造を規定している。
(6)式で入力を0としたときの解をΦとする。系(6)が安定であるとはΦのユークリッドノルム‖Φ‖が一定値を超えないことである。とくに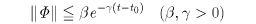
のように指数関数で押さえられる場合は指数的漸近安定という。多変数系の安定判別は非線形系にも用いられるリアプノフLyapunovの判別法が用いられる。
対象系を状態関数で表し、状態量と操作量からなる評価関数を最小化することにより制御系を構成しようとする理論を、最適制御理論という。
制御系の設計はなんらかの評価関数を最適にするように設計される。よく用いられるのは状態変数xおよび入出力uとyの二次式の積分を最小化するもので、レギュレーター問題とよばれる。最適解を求める手法としてはダイナミックプログラミングや最大原理などが用いられている。
[立花康夫]
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...