アポロニウスの円（読み）アポロニウスノエン（その他表記）Apollonius' circle

デジタル大辞泉

アポロニウス‐の‐えん〔‐ヱン〕【アポロニウスの円】

二定点からの距離の比が1ではない一定値である点の軌跡がつくる円。古代ギリシャの数学者アポロニウスによる。

出典　小学館

改訂新版　世界大百科事典

アポロニウスの円 (アポロニウスのえん)
Apollonius' circle

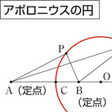
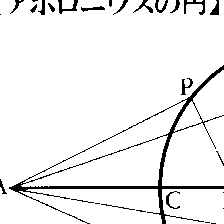
平面上に2点A，Bが与えられたとき，その平面上にあってA，Bからの距離の比が一定であるような点の軌跡は，その比の値が1でなければ，線分ABをその比に内分，外分する点を直径の両端とする円となる。この円をアポロニウスの円と呼ぶ（図1）。古典的な作図問題のもっとも有名なものの一つに，平面上に三つの円が与えられたときに，これらのすべてに接する第4の円を求めよという問題があるが，この第4の円もアポロニウスの円と呼ばれている（図2）。これは一般に8個ある。名はペルゲのアポロニオスの著作に記載されていたことによる。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

アポロニウスの円
アポロニウスのえん

「アポロニオスの円」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典