軌跡（読み）キセキ（その他表記）locus

デジタル大辞泉

き‐せき【軌跡】

１ 車輪の通った跡。轍わだち。
２ 先人の行いの跡。
３ ある人や物事がたどってきた跡。「作家の心の軌跡をたどる」
４ 数学で、点が一定の条件に従って動くときに描く図形。例えば、定点から一定の距離を保ちながら動く点の軌跡は円となる。

出典　小学館

精選版 日本国語大辞典

き‐せき【軌跡】

1. 〘 名詞 〙
2. ① 車のわだちのあと。
3. ② 先人の行ないのあと。手本。また、ある人や物事のたどってきたあと。生活や行為のあと。
   1. [初出の実例]「僕にはこれらの精神的操作の軌跡(キセキ)を詳しくたどれない為に」(出典：僕の語学修業（1949）〈渡辺一夫〉)
   2. [その他の文献]〔後漢書‐逸民伝・高鳳〕
4. ③ 点が一定の条件に従って動くときに描く図形。すなわち、ある条件があたえられたとき、それをみたす点の全体から成る図形。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
5. ④ 物体や粒子などの運動によってできる図形。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

軌跡 (きせき)
locus

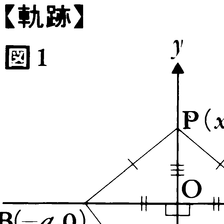
平面上または空間内の図形Mが一定の条件Cをみたす点全体からできているとき，すなわち，〈点Pが図形M上にある〉という命題と〈点Pは条件Cをみたす〉という命題が同値となるとき，図形Mを条件Cをみたす点の軌跡という。軌跡というと，点が動いたときにできる曲線を連想するので，曲線にならない場合は除くように思われがちだが，けっしてそうではなく，上のようにある性質をもつ点全体のことを軌跡といい，軌跡となる図形が何であるかは問わないのである。条件Cをみたす点の軌跡が図形Mであることを証明するには，（1）条件Cをみたすどんな点Pも図形M上にあること，（2）図形M上にあるどんな点Qも条件Cをみたすことの二つを示さねばならない。例えば，〈平面上で2定点A，Bから等距離にあるような点の軌跡は線分ABの垂直2等分線lである〉という定理は次のように証明される（図1）。まず，点PがA，Bから等距離にあれば，線分ABの中点をOとするとき，△AOPと△BOPは3辺の合同となるから，∠AOP＝∠BOP＝90°で，直線POは直線ABと垂直となり，Pはl上にある。次に，Qがl上にあれば，lと直線ABとの交点をOとするとき，△AOQと△BOQは2辺夾角の合同となるから，QA＝QBとなり，QはA，Bから等距離にある。軌跡が曲線の一部分となることもある。例えば，〈平面上に，点Oを中心とする円とこの円外の点Aが与えられたとき，Aを通る直線が円より切りとる弦の中点の軌跡は線分OAを直径とする円の周のうち与えられた円内にある部分である〉（図2）。軌跡という言葉を用いるとき，円や球は平面上または空間内において1定点から一定の正の距離にある点の軌跡ということができる。同様に，放物線は平面上において1定点とこの点を通らない一定直線から等距離にある点の軌跡ということができるし，直円柱面は空間内において一定直線から一定の正の距離にある点の軌跡ということができる。平面上に座標が導入されていれば，x，yについてのある関係式に対し，この関係式をみたす（x，y）を座標とするような点の軌跡が考えられる。これをMとするとき，与えられた関係式はMを表すという。例えば，直交座標の場合，x²＋y²＝r²（r＞0）は原点を中心とし半径がrである円の周囲を表す。解析幾何学は軌跡の問題に対しては非常にすぐれた手法である。なぜならば，ある条件Cをみたす点の軌跡を求めよという問題を解析幾何で扱う場合，条件Cを座標の間の関係式で書き表し，これを計算して簡単な関係式に変形し，この関係式の表す図形が何であるかをみればよいからである。例えば，最初の例で扱った〈平面上2定点A，Bから等距離にある点の軌跡を求めよ〉という問題は次のように解かれる。直線ABを横軸，線分ABの垂直2等分線を縦軸とする座標系を考えるとき，A（a，0），B（－a，0）と表せ，P（x，y）とすれば，条件は（x－a）²＋y²＝（x＋a）²＋y²となるが，これを計算するとx＝0が得られるから，x＝0が表す図形，すなわち線分ABの垂直2等分線が求める軌跡である。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

軌跡
きせき

与えられた条件Cに適する点の集合のつくる図形Fを、条件Cの軌跡という。軌跡は普通、線や面であるが、平面上や空間の領域や空集合になることもある。理論的にいうと、条件Cに適する点の軌跡が図形Fであるというのは、次の二つのことを意味する。(1)Cに適する点はFに属する。(2)Fに属する点はCに適する。

［栗田　稔］

平面上のおもな軌跡

平面上の軌跡には、以下のようなものがある（図）。(1)1点Oから一定の距離rにある点の軌跡は、Oを中心とする半径rの円（円周）である。(2)2点A、Bからの距離が等しい点の軌跡は、線分ABの垂直二等分線である。(3)定直線lへの距離が一定である点の軌跡は、lに平行な2直線である。(4)角の内部にあって角の2辺への距離が等しい点の軌跡は、この角の二等分線である。(5)線分ABを一定の角に見る点の軌跡は、ABを弦とする二つの円弧である。(6)m、nが異なる正数のとき、2点A、Bからの距離の比がm対nである点の軌跡は、線分ABをこの比に内分する点と外分する点を直径の両端とする円（円周）である（アポロニウスの円）。(7)2点F、F′の距離がcのとき、F、F′からの距離の和がcより大きい定数である点の軌跡は、F、F′を焦点とする楕円(だえん)である。また、F、F′からの距離の差がcより小さい定数である点の軌跡は、F、F′を焦点とする双曲線である。(8)1点Fと、これを通らない直線lへ至る距離が等しい点の軌跡は、Fを焦点、lを準線とする放物線である。

［栗田　稔］

空間における軌跡

(1)1点Oから一定の距離rにある点の軌跡は、Oを中心とする半径rの球面である。(2)2点A、Bから等距離にある点の軌跡は、線分ABの垂直二等分面である。(3)1平面pから一定の距離にある点の軌跡は、pに平行な2平面である。(4)二面角（半直線を共有する二つの半平面）への距離が等しい点の軌跡は、この二面角を2等分する平面である。(5)一定の線分ABを直角に見る点の軌跡は、ABを直径とする球面である。

［栗田　稔］

座標と軌跡

座標平面上で、x、yの方程式を満たすx、yを直角座標とする点の軌跡が図形Fのとき、この方程式はFを表すという。x、yの一次方程式は直線を表す。また、空間では、直角座標x、y、zについての一次方程式は平面を表す。

［栗田　稔］

平面上のおもな軌跡〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

軌跡
きせき
locus

与えられた条件 (c) を満たしながら移動する点の集合として得られる図形 F を，(c) を満たす点の軌跡という。軌跡であるためには，(1) (c) を満たす点はすべて図形 F の上にあり，(2) 図形 F 上の点はすべて (c) を満たさなければならない。軌跡は方程式で表わすこともできる。軌跡 F 上の点 (x，y) の満たすべき条件を式で表わしたものを，この軌跡の方程式という。簡単な軌跡の例をあげると次のようなものがある。 (1) 定点から一定距離にある点の軌跡は円である。直交座標系O- xy をとり，定点を原点に重ね，一定距離を r とすると，この軌跡の方程式は，x²＋y²＝r² で与えられる。 (2) 2定点からの距離の平方の差が一定 k² である点の軌跡は直線である。直交座標系O- xy において，2定点の座標を P₁(－a，0)，P₂(a，0) とし，条件を満たす点の座標を P(x，y) とすると，この軌跡は，x＝±k²/4a の方程式で表わされる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

軌跡【きせき】

一定の条件を満足しながら動く点や線が描く図形。図形Fが条件Aを満たす軌跡であることを証明するには，1.Aを満たす任意の点はF上にある（必要条件），2.F上の任意の点はAを満たす（十分条件），の二つを証明しなければならない。
→関連項目曲線｜放物線

出典　株式会社平凡社

普及版 字通

【軌跡】きせき

軌迹。

字通「軌」の項目を見る。

出典　平凡社「普及版 字通」