ガウス=ラプラスの定理（読み）ガウスラプラスのていり（英語表記）Gauss-Laplace theorem

改訂新版　世界大百科事典

ガウス=ラプラスの定理 (ガウスラプラスのていり)
Gauss-Laplace theorem

これはド・モアブル=ラプラスの定理ともいい，古くから知られているもっとも重要で基本的な確率論の極限定理の一つである。成功する確率がpであるn回のベルヌーイ試行において，成功する回数S_nは二項分布に従う。すなわちP（S_n＝k）＝_nC_kp^kqⁿ⁻^k（ただしq＝1－p）。これからかってな定数aとb（＞a）に対して，n→∞のときP（np＋a\(\sqrt{npq}\)＜S_n＜np＋b\(\sqrt{npq}\)）はN（b）－N（a）に近づく。ここにN（x）は標準ガウス分布関数である。すなわち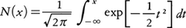，このことは適当に尺度を変えると，S_nは平均値npの近くで正規分布に近いことを示す。この近似で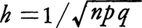が微小とはいいがたいときは，図からわかるように，S_nの分布のN（x）による近似には補正が必要である。例えばn＝100，p＝0.3のとき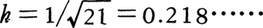で微小ではない。よってp（27≦Sn≦33）＝P（－3h≦Sn－30/\(\sqrt{21}\)≦3h）≒N（3.5h）－N（－3.5h）＝0.55……とすればよい。
→中心極限定理
執筆者：飛田 武幸

図－ガウス=ラプラスの定理

出典　株式会社平凡社「改訂新版　世界大百科事典」