中心極限定理（読み）チュウシンキョクゲンテイリ

デジタル大辞泉

ちゅうしんきょくげん‐ていり【中心極限定理】

母集団から無作為にn個の標本を抽出することで得られる標本平均の分布は、nが大きくなるにしたがって、正規分布に近づくという定理。すなわち、母集団の確率分布によらず、同じ平均と分散で表される正規分布で近似できることを示す。

出典　小学館

日本大百科全書(ニッポニカ)

中心極限定理
ちゅうしんきょくげんていり

確率変数Snの確率分布が二項分布B(n,p)であるとすると、

は、ベルヌーイの大数(たいすう)の法則によって、nが大きいとき、例外的な場合を除いてほぼ0に近い。しかしSn-npをnで割るかわりに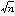で割ったものについてはどうか。これについては次の定理がある。

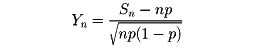
と置けば、Ynの確率分布は、nが十分大きいとき正規分布N(0,1)に近い。すなわち、任意の実数a,b(a＜b)に対して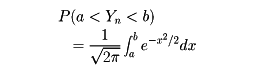

が成り立つ。この定理をラプラスの定理またはド・モアブル‐ラプラスの定理という。これは、ベルヌーイの大数の法則を実用的な形にまで拡張したものである。

　ラプラスの定理における二項分布の仮定を取り除いても同じような形の次の定理が成り立つ。確率変数X₁、X₂、……、X_nが独立であって、各X_iは平均値がm、分散がσ²であるような同一の確率分布をもつとする。このとき

と置けば、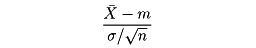

の分布は、nが十分大きいときには正規分布N(0,1)に近い。この定理を中心極限定理という。この定理は種々の方向に拡張されるが、これら一連の定理も中心極限定理とよばれている。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

中心極限定理 (ちゅうしんきょくげんていり)
central limit theorem

多数の偶然現象について，その極限的性質を述べたいろいろな確率論の定理があるが，これは理論的にも，また実際面への応用上からも最も重要な定理である。確率変数についていえば，X₁，X₂，……，X_nは独立で同じ分布に従うとし，それぞれの平均値をm，標準偏差をσとする。和の平均値はnm，標準偏差は\(\sqrt{n}\)σとなる。中心極限定理は，S_nを規格化したもの，すなわち（S_n－nm）/\(\sqrt{n}\)σの分布は，nが大きければ標準正規分布に近いことを主張している。とくにS_nが二項分布にしたがうときに詳しくいえば，nが大きいときS_nがk₁とk₂（k₁＜k₂とする）の間の値をとる確率は，標準正規分布においてにほぼ等しい（pは着目する事象の起こる確率，qはその余事象）。この近似は，npqが大きいほどよく（npqを少なくとも3以上にとれという説がある），また平均値の近くでよくあてはまっている。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

中心極限定理
ちゅうしんきょくげんていり
central limit theorem

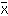統計学で取り扱う母集団の確率分布は，そのほとんどが正規分布に従っている。その根拠を与えるのが，中心極限定理である。すなわち「母平均がμ，母分散がσ²の母集団において，そのなかから n 個の標本をとったときの標本平均 の分布 は，n を十分大きくとると，母集団の分布とは無関係に，正規分布に近似する」というものである。このことから，確率変数 N（μ，σ²/n）の分布が，n→∞のとき，正規分布 N（0，1）に収束するという結果を得る。これを中心極限定理ということもある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の中心極限定理の言及

【確率論】より

…こうした基礎のうえに確率論は極限定理，確率過程論，数理統計学への応用等々数学の一分野として確立された。　同じ分布に従う独立な確率変数の和を規格化(平均値を0に，分散を1にするよう適当な数を引いたり割ったりすること)すれば，変数の個数が多いときその分布は標準正規分布に近いとする中心極限定理，また関連した極限定理はソ連のヒンチンA.Y.Khintchin(1894‐1959)をはじめ多くの学者によって研究された。また時間の推移とともに変化する偶然現象を扱う確率過程の研究は，近代確率論のもっとも重要な課題となっている。…

【数理統計学】より

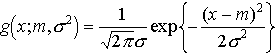…実際，前述の解熱剤の例でいえば，その効果は下がった体温の量で表され，基本的にはある定まった値(平均値m)であるが，患者の体質や病状などに個人差があって，mからの偶然誤差が生ずる。この誤差の分布は，中心極限定理の教えるところによって正規分布と仮定するのが妥当であることがわかる。解熱剤の平均的効果を知るには，得られた標本からmの値を推定することになる。…

【標本調査】より

…この信頼係数を知るためには，一般には，母集団の各要素の値が未知の場合にも標本平均の分布がわからなければならない。これを保証するのが中心極限定理である。この定理によると，母集団の分布がどんな形をしていてもその平均μと分散σ²が既知なら，無作為に数多くの標本をとりさえすれば，標本平均は近似的に母平均μに一致する平均をもち，分散σ²/nをもつ正規分布に従う。…

※「中心極限定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」