尺度（読み）シャクド（その他表記）scale

デジタル大辞泉

しゃく‐ど【尺度】

１ 物の長さを測る道具。ものさし。
２ 長さ。寸法。「尺度を測る」
３ 計量の標準。また、判断・評価などの基準。「合否判定の尺度を決める」
[類語]基準・標準・物差し・水準・レベル・規準・定規・本位・程度

出典　小学館

精選版 日本国語大辞典

しゃく‐ど【尺度】

1. 〘 名詞 〙
2. ① 長さをはかる器具。矩尺(かねじゃく)、鯨尺、曲尺(まがりがね)、巻き尺、メートル尺などがある。ものさし。また、計量の標準。
   1. [初出の実例]「二書猶_二権衡尺度_一乎」(出典：童子問（1707）下)
   2. 「家光は聰明果断の主にして〈略〉鋳銭の事、尺度権衡の事、亦た此時に定まれり」(出典：日本開化小史（1877‐82）〈田口卯吉〉五)
   3. [その他の文献]〔宋書‐律志〕
3. ② 物の寸法や長さ。また、その度合。
   1. [初出の実例]「或は梯尺に依ることなく距離及尺度の如きは数字を以て注記するに止むる」(出典：作戦要務令（1939）一)
4. ③ 転じて、物事の評価、判断を行なう際の規準。めやす。
   1. [初出の実例]「強ひて自己の感覚を尺度として他を律するは謬なるべし」(出典：邪宗門（1909）〈北原白秋〉例言)

せき‐ど【尺度】

1. 〘 名詞 〙 ( 「せき」は「尺」の漢音 ) ＝しゃくど（尺度）

出典　精選版 日本国語大辞典

最新 心理学事典

しゃくど
尺度
scale

尺度とは，対象に数値を対応させる規則およびその規則によって与えられる数値である。尺度は，その性質により名義尺度，順序尺度，間隔尺度，比尺度などの尺度の水準scale type,measurement levelに分類される。名義尺度nominal scaleは，野球選手の背番号のように，数値は対象を区別するために用いられる。しかし，数値の大小関係が対象の特性の強弱に対応しているわけではない。背番号3番の選手が背番号1番の選手より3倍優秀であるということではない。順序尺度ordinal scaleでは，対象の特性の強さの順序に対応するように数値が対応づけられる。しかし，いくつかの可能な職種に対する選好を順序によって表わすとき，1番目の職種，2番目の職種の選好の差は，2番目の職種と3番目の職種の選好の差と等しくない。間隔尺度interval scaleでは，順序尺度の条件に加えて，数値の差も意味をもつ。数値の差が等しいとき，対象の特性強度の差も同じである。温度において，セ氏で表わした10℃と20℃の差および30℃と40℃の差はいずれも10℃の差で等しく，これをカ氏で表わしても50℉と68℉および86℉と104℉で，いずれも18℉の差となりカ氏でも同じである。温度を表わすセ氏あるいはカ氏は，その数値の表わす差は温度の差としての物理学的意味をもつ。しかし，数値0は，その表わす特性（温度）の量がないことを意味しない。セ氏0℃はカ氏32℉である。比尺度ratio scale（比率尺度ともいう）では，間隔尺度の条件に加えて数値の比も意味をもつ。長さを㎝あるいはｍを単位として表わすとき，0㎝あるいは0ｍは長さがないことを表わす。また，10ｍは5ｍの2倍であるが，これを㎝を単位として1000㎝および500㎝と表わしたときも数値は2倍になっている。物理量として，10ｍの長さは5ｍを二つ連結したものとして意味がある。

　尺度の水準に対応して有意味な統計量が決まる。たとえば，順序尺度では平均値は意味をもたない。5個の作品ａ，ｂ，ｃ，ｄ，ｅの評価が10点満点で1点⒜，3点⒝，5点⒞，6点⒟，10点⒠であったとき，平均値は5点で作品ｃが平均値に対応する。しかし，作品の優劣の順序はそのままで1点⒜，7点⒝，8点⒞，9点⒟，10点⒠となるような甘い評価が行なわれると，平均値は7点で作品ｂが対応する。1点⒜，2点⒝，3点⒞，4点⒟，10点⒠と辛い評価のときは，平均値は4点で作品ｄが平均値に対応する。しかし，上の例において，中央値に対応する作品はつねにｃである。順序尺度では，尺度値の順序関係が保たれていても，その平均値に対応する対象は尺度に応じて変わる。しかし，中央値は尺度によらず同じ対象に対応する。これに対して，間隔尺度および比尺度では，平均値も有意味な統計量である。

　尺度は，量的研究法において重要な役割を担うものであり，その理論的研究は主に計量心理学の領域で行なわれている。尺度の構成法は，精神物理学（心理物理学）psychophysics的方法，質問項目によるもの，テスト理論に基づくもの，複数の次元についての尺度を同時に求める多次元尺度法などがある。

　精神物理学における尺度は，マグニチュード推定尺度，JND尺度，カテゴリ尺度の3種類が区別される。メタセティック連続体metathetic continuumとよばれる感覚では，これら3種類の尺度は直線関係にあり，同じものを表わしていると考えられているが，プロセティック連続体prothetic continuumでは，尺度値を物理量の関数として表わしたとき異なる関数形となり，3種類の尺度の関係は非線形である。プロセティック連続体においては，尺度値を物理量の関数として表わしたとき，マグニチュード推定尺度はベキ関数，JND尺度は近似的に対数関数，カテゴリ尺度はベキ関数と対数関数の間の形を取るとされている。

　質問項目を用いる尺度の種類としては，サーストン・スケールThurstone scale，ガットマン・スケールGuttman scale，およびリッカート・スケールLikert scaleが挙げられる。このうちサーストン・スケールやガットマン・スケールでは，与えられた項目群から適当な項目を選択する形式の質問紙を想定している。サーストン・スケールでは，各項目は尺度の対象となる特性のある量にそれぞれ対応している。項目ｉが特性の量ｖⁱに対応しているとき，調査対象の人が項目ｉ¹，…，項目ｉ^kを当てはまるものとして選べば，それらの項目の値の代表値，平均値あるいは中央値をその人の尺度値とする。項目ｉの値ｖⁱは，尺度の作成において等現間隔法により与えられている。

　ガットマン・スケールでは，各項目は特性の量に対応して順序づけられている。たとえば項目ｉと項目ｊがこの特性の量に応じて一次元上に位置づけられているとき，項目ｊを選んだ人は項目ｉも選ぶことが期待されている。サーストン・スケールの場合は，その人の特性の強さに対応する項目のみを選ぶことが想定されているが，ガットマン・スケールでは選ばれた項目より弱い項目はすべて選ばれるように作成される。学力テストなどにおいて難しい問題を解いた人は，それよりやさしい問題はすべて解けるという想定である。

　リッカート・スケールでは，特性の強さを測るために用意された項目について，たとえば「よく当てはまる」，「当てはまる」，「どちらかといえば当てはまる」，「どちらかといえば当てはまらない」，「当てはまらない」，「まったく当てはまらない」と選択肢を設定して，最も適切なものを選ばせる。各選択肢は，「よく当てはまる:1点」，「当てはまる:2点」，…というように点数が割り振られており，各項目に対して選ばれた選択肢の点数がその項目の得点として与えられ，それらの平均値などが尺度の値として用いられる。

　リッカート・スケールにおいて，項目ｉの点数Ｘⁱをその人の特性の量（真値）Ｔⁱとランダムな変動分（誤差）Ｅⁱとの和



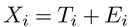
で表わしたとき，項目の点数の和は



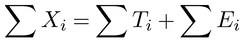
と表わされる。得点和ΣＸⁱに占めている特性の真値の和ΣＴⁱの割合を，それらの分散（Var）の比で表わしたものは，信頼性係数とよばれている。



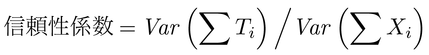
　信頼性係数の推定値としてよく用いられているものにクロンバックのα係数がある。

　尺度の安定性を，その一般化の観点からとらえるものに一般化可能性理論generalizability theoryがある。得点に対して，評定される人ｐ，評定する人Ｒ，評定項目Ｔなどの要因に分けて分散分析の考え方を適用し，母集団における各要因の分散パラメータの推定値が求められる。これらの推定値に基づいて，いろいろなテスト構成における比（真値の分散／和得点の分散）が一般化可能性係数として算出され，適切なテスト構成が決められる。

　テスト理論では，ガットマン・スケールの各項目に対して，特性量の関数として各項目のYes（あるいは正答）の確率を表わす項目特性関数を求める項目反応理論item response theory（IRT）に基づく尺度構成がある。個々の人に対する特性量の推定は，項目に対する反応パターンから項目特性関数に基づいて行なわれる。

　一つの対象について複数の次元の尺度値を求めるものに，多次元尺度法multidimensional scaling（MDS）がある。対象間の関係を，対象に対する各尺度の値を座標値とする点の空間関係で表わし，データとして得られた対象間の関係から座標値として尺度値が求められる。複数の尺度の分析にかかわる統計分析法としては，因子分析法がある。一つの質問項目群を各因子に対応するグループに分け，各グループから一つの尺度（たとえばリッカート・スケール）が構成される。

　尺度の使用においては，その尺度値の安定度を表わす信頼性係数が十分高いかどうかということのほかに，尺度値が測ろうとしている特性を適切に測っているのかどうかの問題がある。たとえば，学力を頭部の前後方向最大直径値で推定した場合，直径は物理量で安定しているので信頼性係数は高いと予想される。しかし，直径の値が構成概念としての学力の尺度値としてどの程度適切であるかは問題である。この尺度が測るべきものを正しく測っているかどうかは，妥当性validityの問題として扱われる。すなわち，尺度の妥当性とは，実証データと理論が，その尺度の使用目的に照らし合わせて，尺度値の解釈を支持する度合いを表わす。尺度の開発および使用においては，信頼性と妥当性を考慮しなければならない。　→質問紙法　→信頼性　→精神物理学的測定法　→多次元尺度法　→妥当性
〔岡本 安晴〕

出典　最新 心理学事典

日本大百科全書(ニッポニカ)

尺度
しゃくど

物の長さを計るため、約束によりまたは制度として定められた単位、またはそれで目盛られた物差しのこと。長さは人間が最初に計ることを始めた量で、最初は手幅、肘(ひじ)の長さ、指幅、両手を広げた長さ、足の長さ、歩幅などで直接計られたが、やがてこれらが棒や板に移され、もとの身体の部分の大きさは単位となった。この発展の過程は、近代的制度の単位の名に、たとえばフートfoot（足）などが残っているのをみてもわかる。やがて国家が形成されると、これらの尺度を統一し、しかも変化しないように標準を定める必要がおこり、こうして尺度は制度として定められる。メートル法は国際的な統一のために設けられたものである。尺度はまた物事の評価の基準の意味においても用いられる。

　広い意味の尺度には、次の種類があり、通常の測定における重要な役割を果たしている。

(1)比尺度（比例尺度）：数値の差および比、すなわち加減乗除の演算に意味をもつ尺度。たとえば長さ、質量など。

(2)間隔尺度：数値の差のみに意味をもつ尺度。たとえばカレンダーの日付、セルシウス温度など。

(3)順序尺度：数値の大小関係のみに意味をもつ尺度。たとえばレースの着順、モース硬度など。

(4)名義尺度：単なる区別のために用いる尺度。順序もなく、加減の演算もできない。たとえば背番号、電話番号など。

［小泉袈裟勝・今井秀孝］

[参照項目] | 単位 | はかる | 物差し

出典　小学館　日本大百科全書(ニッポニカ)

普及版 字通

【尺度】せきど

ものさし。

字通「尺」の項目を見る。

出典　平凡社「普及版 字通」

ブランド用語集

尺度

尺度とは変数と数値を対応させる基準のことをいう。

出典　(株)トライベック・ブランド戦略研究所