コーシーの積分定理（読み）コーシーのせきぶんていり（その他表記）Cauchy's integral theorem

ブリタニカ国際大百科事典 小項目事典

コーシーの積分定理
コーシーのせきぶんていり
Cauchy's integral theorem

コーシーの基本定理または単にコーシーの定理ともいう。複素変数の関数 f(z) が，複素平面上の単一閉曲線 C で囲まれた領域 D およびその周である C 上で連続，かつ D で正則ならば，積分路を C に沿って1周するようにとれば，
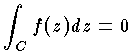が成り立つ。これをコーシーの積分定理という。ここで C の内部の任意の1点を z とすると，
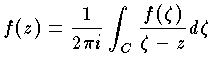が成り立つ。これをコーシーの積分表示という。これは，正則な関数の1点 z における値が，その点を内部に含む単一閉曲線 C 上の関数 f の値によって，完全に決定されることを表示する式である。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

コーシーの積分定理 (コーシーのせきぶんていり)

→関数論

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のコーシーの積分定理の言及

【関数論】より

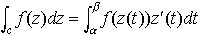…この右辺は，f(z(t))z′(t)＝U(t)＋iV(t)と，実部，虚部に分けて得られる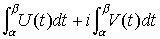のことである。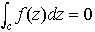
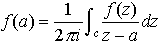［コーシーの積分(基本)定理］
　fが滑らかな単純閉曲線Cとその内部Dで正則ならば，
［コーシーの積分公式］
　f,C,Dは上と同じとし，さらにCはDを左にみてまわっているとき，任意のa∈Dに対し，　以上の二つは次のような一般化ができる。領域Dの境界Cは，Dを左にみてまわる単純閉曲線C₁，……，C_nから成っているとき(図1)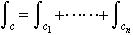，と解釈して，上述の二つの式が成り立つ。…

※「コーシーの積分定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」