精選版 日本国語大辞典 「関数論」の意味・読み・例文・類語
かんすう‐ろんクヮンスウ‥【関数論】
改訂新版 世界大百科事典 「関数論」の意味・わかりやすい解説
関数論 (かんすうろん)
theory of functions
複素関数論ともいい,数学の中の解析学の一つの分野である。独立変数と従属変数が複素数であるような関数を複素関数というが,関数論はそのうち正則関数およびそれに関連する関数を対象とする。独立変数が2個以上のときは,とくに多変数関数論という。ここでは,w,zともに複素数である1変数関数w=f(z)の関数論を解説する。
歴史
解析学において複素数を用いるという考えは,微分積分学の発見の直後からあったようであるが,これが盛んに用いられるようになったのは18世紀になってからである。L.オイラーは公式eiθ=cosθ+isinθを導いたり,複素数の対数についてその多価性を発見したりしている。また,オイラーやA.C.クレーローは,流体力学を論ずるのに複素線積分を用いて,今日,コーシー=リーマン方程式と呼ばれる関係式を導いている。けれども,このころは,実関数に関する二つの式を複素関数を用いて一つの式で表すといった便宜的なものにすぎなかった。
関数論の基礎は,19世紀の中ごろに,A.コーシー,G.リーマン,K.ワイヤーシュトラスの3人によって築かれた。
コーシーは1814年に書いた論文(1825発表)において,流体力学の考えに基づいて複素積分を考え,それを実定積分の計算に応用している。次いで,留数定理,積分公式などを発見し,51年までの間に正則関数の概念を確立した。彼の理論はただちに数学界に認められ,当時の主要分野をなしていた楕円関数の研究にとり入れられた。
リーマンは51年の学位論文において,複素微分可能性によって正則関数を定義し,ガウスによる等角写像の考え(1822)を発展させた。さらに,いわゆるリーマン面を導入して,楕円関数論をアーベル関数論に飛躍させた。リーマン面の導入は,また,位相幾何学の出発点をなすものでもあった。同じころ,ワイヤーシュトラスは,べき級数をもとにして(これは18世紀のJ.ラグランジュの考えの復活である),解析接続によって解析関数の概念を確立し,楕円関数論に新しい境地を開いた。彼は,また,アーベル関数を論ずるにあたって,多変数関数論の基礎づけにも大いに貢献している。
正則関数
複素平面の領域Dに属する全複素数に,複素数を一つ対応させる対応fを,Dを定義域とする複素関数という。w=f(z)とも表す。実部と虚部を用いてz=x+iy,w=u+ivと表せば,
f(z)=u(z)+iv(z)=u(x,y)+iv(x,y)
によって,2変数の実関数uとvが定まり,逆にそのようなu,vから複素関数fが定まる。
z0∈Dにおける複素微分係数を,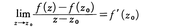 によって定義する。これが存在するとき,fはz0で複素微分可能という。Dのすべての点で複素微分可能なときfはDで正則であるという。
によって定義する。これが存在するとき,fはz0で複素微分可能という。Dのすべての点で複素微分可能なときfはDで正則であるという。
正則とは,⊿z→0に対する⊿w/⊿zの極限値が,⊿zのとり方によらずに一定であるということを意味する。このことは,とくにf′(z0)≠0のとき,fの与える写像が局所的に等角写像となっていることと同値である。
fが複素微分可能であるためには,uとvが連続な偏導関数をもち,それらが,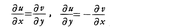 という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。このことによって,とくにuとvは調和関数となる。
という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。このことによって,とくにuとvは調和関数となる。
正則関数の例
複素微分係数の定義は,形式上は微分積分での微分係数と同じであるので,和や積などの微分については実関数と同じ扱いができる。例えば,多項式や有理式は,分母が0とならないところで正則である。べき級数の和はその収束円内で正則で,べき級数を用いることによって,複素変数zに対する指数関数と三角関数を次のように定義する。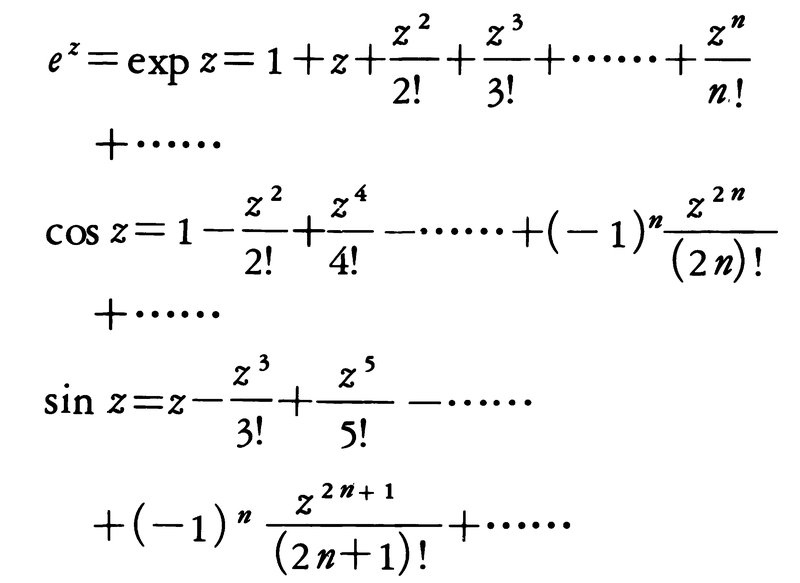
これらは複素平面Cで正則である。zが実数のときは既知のものと一致する。また,指数関数と三角関数の間に次の関係があることがわかる。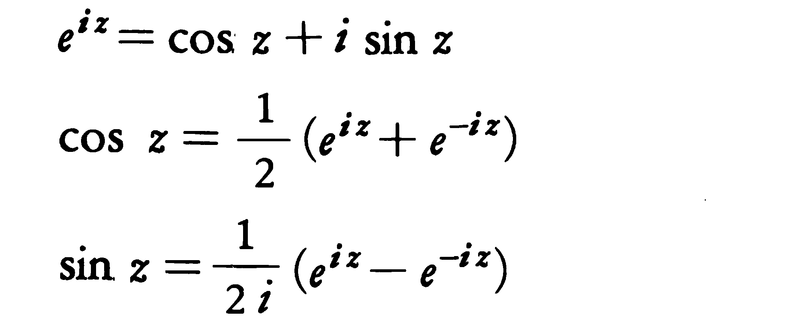
複素数aおよびbに対しても指数法則ea⁺b=eaebは成り立ち,三角関数に対する加法定理は,すべてこれから導き出される。
複素数z≠0の対数は次のように定義する。z=reiθを満たすr>0と任意のθによって,
logz=logr+iθ
一つのzに対して,θは2πの整数倍の差をもつ無限個の値があるから,logzは多価関数である。-π<θ≦πに制限して一つの価をとらせたものを,logzの主値という。zが正の実数のとき,logzの主値は実関数としての対数関数の値と一致する。
累乗根はzα=eαlogzで定めるが,logzの多価性に応じて,zαも一般には多価である。
多価関数は,リーマン面を考えることによって,そこで1価となるようにできる。
以上で定義された関数を初等関数という。
そのほか,楕円関数,Γ関数,ζ関数をはじめ,数学の各分野に“自然に”現れる関数の多くは,変数を複素数に拡張することによって正則関数となる。
積分定理
複素関数f(z)=u(z)+iv(z)が領域Dで連続なとき,D内の滑らかな曲線C:[α,β]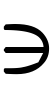 t
t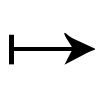 z(t)=x(t)+iy(t)∈Dに沿う複素線積分を次の右辺で定義し,左辺の記号で表す。
z(t)=x(t)+iy(t)∈Dに沿う複素線積分を次の右辺で定義し,左辺の記号で表す。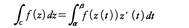 この右辺は,f(z(t))z′(t)=U(t)+iV(t)と,実部,虚部に分けて得られる
この右辺は,f(z(t))z′(t)=U(t)+iV(t)と,実部,虚部に分けて得られる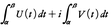 のことである。
のことである。
コーシーの積分(基本)定理
fが滑らかな単純閉曲線Cとその内部Dで正則ならば,
コーシーの積分公式
f,C,Dは上と同じとし,さらにCはDを左にみてまわっているとき,任意のa∊Dに対し,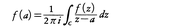
以上の二つは次のような一般化ができる。領域Dの境界Cは,Dを左にみてまわる単純閉曲線C1,……,Cnから成っているとき(図1),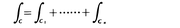 と解釈して,上述の二つの式が成り立つ。
と解釈して,上述の二つの式が成り立つ。
これらの定理から,数え切れないくらい多数の定理が導かれる。以下,直接に導かれることの例をいくつかあげる。
(1)正則関数は,定義域に含まれる円内でべき級数に展開できる。
(2)正則関数は何回でも複素微分可能である。
(3)単連結領域で正則な関数fは原始関数F,すなわちF′=fを満たす正則関数Fをもつ。
(4)最大値の原理 領域Dで定義された正則関数の絶対値が,Dの1点で最大値をとるならば,fは定数でなければならない。したがって,Dが有界でfがDの境界も込めて連続ならば|f|の最大値はDの境界でとられなければならない。
(5)リウビルの定理Liouville's theorem 複素平面Cで正則で有界な関数は,定数以外には存在しない。
また,(1)から次の定理が導かれる。
(6)一致の定理 領域Dで正則な関数fとgが,Dに少なくも一つの集積点をもつ部分集合で一致するならば,D全域で一致しなければならない。
一致の定理を基礎にして解析接続が考えられ,それによってワイヤーシュトラスの解析関数が定義できる。
留数定理
DとC1,……,Cnはコーシーの基本定理の場合と同じとし,fはD内に有限個の孤立特異点a1,……,apをもち,それら以外のD∪C1∪……∪Cnでは正則であるとする。すると,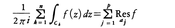 が成り立つ。ここで
が成り立つ。ここで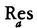 はaにおける留数を表す。これを留数定理というが,コーシーの積分(基本)定理の拡張である。特異点がなければ上式の右辺は0となるが,特異点があるため0にならずに“残りもの”が生ずる。これが,留数という名の由来であるとされる。
はaにおける留数を表す。これを留数定理というが,コーシーの積分(基本)定理の拡張である。特異点がなければ上式の右辺は0となるが,特異点があるため0にならずに“残りもの”が生ずる。これが,留数という名の由来であるとされる。
コーシーはこの定理を定積分の計算に応用した。例えば,f(z)=eiz/(z2+c2)は点±ciに特異点をもち,そこでの留数はe⁻c/2ciである。よって,図2の半円周Cで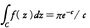 が成り立つ。この両辺の実部をとり,Cの半径を→∞とすると,円周部の積分は0に収束するので,直径部の積分のみから,
が成り立つ。この両辺の実部をとり,Cの半径を→∞とすると,円周部の積分は0に収束するので,直径部の積分のみから,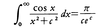 を得る。
を得る。
関数の展開
複素平面Cにおいて,孤立特異点a1,a2,……をもつ正則関数f(z)が与えられたとする。点akにおけるローラン展開の主要部をPk(z)としたとき,多項式pk(z)とCで正則なg(z)を,f(z)=Σ(Pk(z)-pk(z))+g(z)が成り立つようにとることができる。これをfの部分分数展開という。例えば,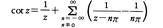
ここでは,ちょうどg≡0となっている。なお,この式は整理して,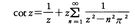 とできる。
とできる。
次にCの正則関数f(z)が与えられており,a1,a2,……で値が0になり,ほかでは0にならないものとする。このとき,整数ν,qkと正則関数g(z)を,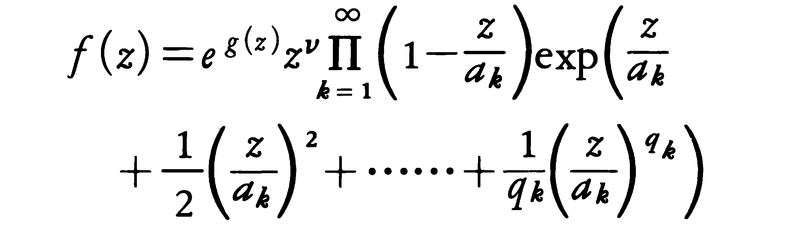
が成り立つようにとることができる。これをfの因数分解という。例えば,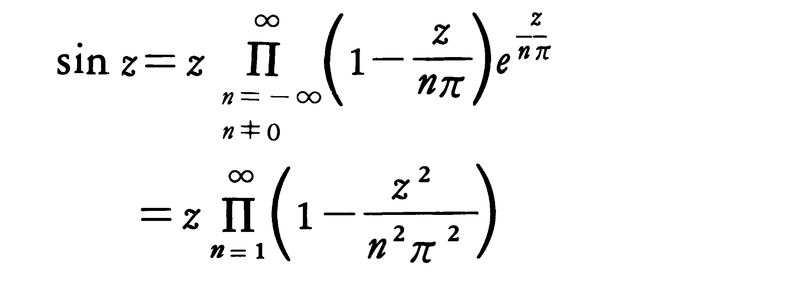
無限遠点
複素平面に,新たに1点をつけ加えてΣとおく。つけ加えられた点を無限遠点と呼び,記号∞で表す。そして,発散する複素数列{zn}でlim|zn|=∞であるものを〈無限遠点に収束する〉と定義して,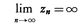 と表す。
と表す。
こうしてつくられたΣを具体的に表現するには,複素平面に原点で接する球面を利用する。図3のように接点をS,そこを通る直径の他の端点をNとおく。Nから複素平面の点zに至る線分をとり,それと球面との交点をPとおく。すると対応z Pが得られるが,これを立体射影という。これは複素平面から,Nを除いた球面の上への1対1対応を与えており,しかも|z|→ ∞のときPはNに限りなく近づく。だから,複素平面につけ加えられた無限遠点はNに対応するものと考えられ,その意味でΣは球面そのものと考えられる。このような理由に基づいてΣをリーマン球面という。
Pが得られるが,これを立体射影という。これは複素平面から,Nを除いた球面の上への1対1対応を与えており,しかも|z|→ ∞のときPはNに限りなく近づく。だから,複素平面につけ加えられた無限遠点はNに対応するものと考えられ,その意味でΣは球面そのものと考えられる。このような理由に基づいてΣをリーマン球面という。
リーマン球面の領域Dで定義された複素数値関数は,次の条件を満たすときDで正則であるという。D-{∞}では前述の意味で正則であり,さらに∞の近傍r<|z|≦∞がDに含まれるとき,関数,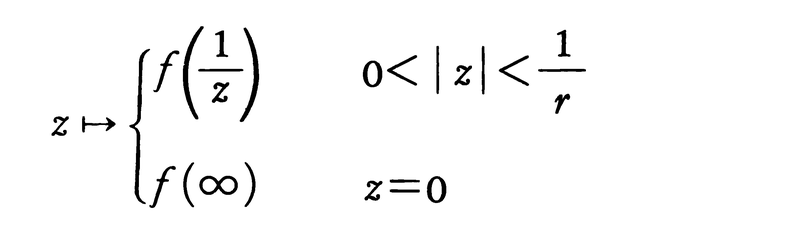
が|z|<1/rで前述の意味で正則である。
リーマン球面の領域における正則関数に対しても,最大値の原理や一致の定理が成り立つ。
超越整関数,超越有理型関数
複素平面Cで正則な関係を整関数といい,そのうちで多項式でないものを超越整関数という。これは無限遠点に真性特異点をもつものと考えられる。超越整関数fは,たかだか一つの値を除きすべての複素数値を無限回とる(ピカールの定理Picard's theorem)。Cで有理型であって有理式でない関数を,超越有理型関数という。ピカールの定理を用いると,たかだか二つを除いたすべての値b∈C∪{∞}を無限回とることがわかる。
この結果を精密化し,統一的に扱う理論が,1930年代にネバンリンナR.Nevanlinnaによって建設された有理型関数の値分布論で,近代関数論の出発点となった。
執筆者:及川 廣太郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「関数論」の意味・わかりやすい解説
関数論
かんすうろん
関数の考えを、複素数zを変数とし、複素数の値をとる関数にまで広げて、微分や積分を考えると、普通の微分・積分と違った、おもしろい、また役にたつ性質をもつばかりでなく、微分・積分の定理を統一的に考えることができるようになる。このような数学の研究領域を関数論または複素関数論といい、フランスのコーシー、ドイツのリーマン、ワイアシュトラースらによって始められた。
w=f(z)を複素平面の、ある領域Dで定義された複素数の値をとる関数とし、z0における微分係数を(極限値が存在するとき)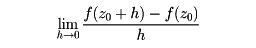
によって定義し、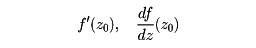
などと表す。この定義は、普通の微分における定義と同じであるが、複素数を実部と虚部に分けて、
z=x+iy, f(z)=u(x,y)+iv(x,y)
と表すと、z0=x0+iy0において微分可能になる必要十分条件は、2変数(x,y)の関数と考えたu(x,y), v(x,y)が(x0,y0)で全微分可能、しかも、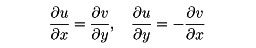
が成り立つことである(コーシー‐リーマンの微分方程式)。
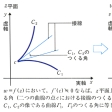
領域Dの各点で微分可能なとき、この関数はDにおいて正則であるという。複素関数w=f(z)は、複素平面の点z=x+iyをw=u+ivに写す変換と考えられるが、正則関数の一つの性質として、f′(c)≠0ならば、点cを通る二つの曲線C1、C2はw平面のf(c)を通る二つの曲線Γ1、Γ2に写されるが、このとき、cにおいてC1、C2のつくる角は、f(c)において、Γ1、Γ2のつくる角に等しい()。この性質を正則関数の表す変換の等角性といい、流体力学、電磁気学などで利用される。
領域D上の正則関数f(z)の積分を次のように定義する。D内に値をとる滑らかな曲線Cをz(t) ; a≦t≦bと表すとき、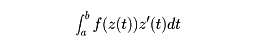
を、曲線Cに沿っての積分といい、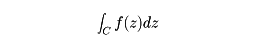
と書く。CがD内の単純閉曲線ならば、とくに、コーシーの積分定理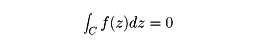
が成り立つ。これから、正則関数の多くの有用な定理が導かれる。たとえば、Cの内部にある点cに対し、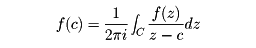
が成り立ち(コーシーの積分定理)、これから、正則関数は何回でも微分可能であり、テーラー展開ができて、cの近くで、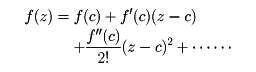
と表されることがわかる。閉曲線C内に正則でない点(特異点という)aがあるとき、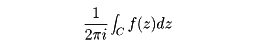
は0になるとは限らない。aがC内のただ一つの特異点のとき、上の値を関数f(z)のaにおける留数(りゅうすう)という。留数は積分の値を計算しなくても、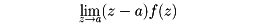
が有限確定ならば、この値がaにおける留数に等しい。したがって、この極限値を用いて積分の値を求めることができる。
これは、普通の実関数の定積分を求めるのによく用いられる。
[洲之内治男]
百科事典マイペディア 「関数論」の意味・わかりやすい解説
関数論【かんすうろん】
→関連項目解析学|実変数関数論|楕円関数|等角写像|ピカール|リウビル
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「関数論」の意味・わかりやすい解説
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の関数論の言及
【コーシー】より
…ことにコーシーの名を数学史上不朽のものにしたのは,複素数を変数とする関数の線積分に関するもので,1814年から50年にかけてはぐくまれたものである。後世,関数論と名付けるものを基礎づけたもので,このときに樹立されたものを関数論における基本定理と名付けている。【小堀 憲】。…
※「関数論」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...