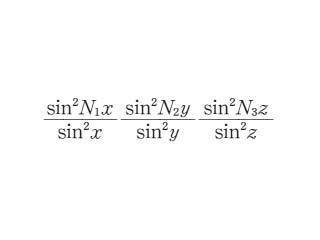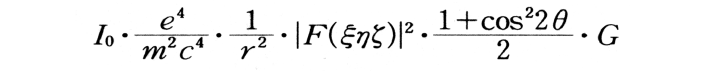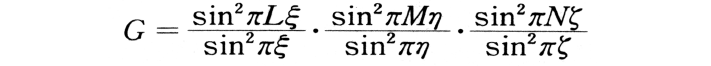ラウエ関数（その他表記）Laue's function

法則の辞典

ラウエ関数【Laue's function】

結晶を平行六面体と考え，それぞれの稜の長さを N₁a，N₂b，N₃c（N₁，N₂，N₃ は正の整数），X線の波長を λ，入射X線を S₀，反射X線を S とし，h，k，l を0を含む任意の整数（ミラー指数＊）としたとき，X線の回折強度は

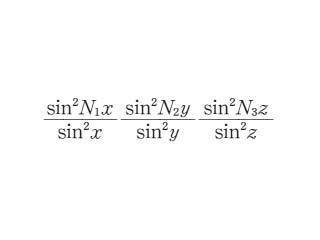
に比例する．ただし x＝（π/λ） ｛a（S－S₀） ｝，y＝（π/λ） ｛b（S－S₀） ｝，z＝（π/λ） ｛c（S－S₀） ｝，である．この関数がラウエ関数と呼ばれるものである．これから結晶が十分に大きい場合，すなわち N₁，N₂，N₃ が大きくなると

a（S－S₀）＝hλ，b（S－S₀）＝kλ，

c（S－S₀）＝lλ

を満足するときのみ強いX線回折像が生じることがわかる．これが，ラウエの条件＊にほかならない．

出典　朝倉書店

最新 地学事典

ラウエかんすう
ラウエ関数

Laue function

強度I₀のX線が3稜の長さがLa，Mb, Ncなる平行六面体の結晶に入射したとき回折されるX線の結晶から距離rの点における強度I（ξηζ）は，

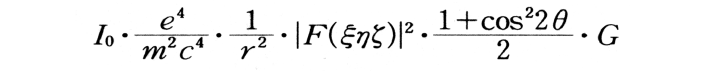
ただし，

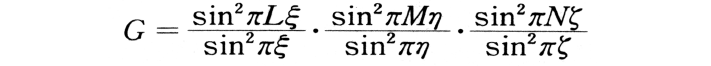
e, mはそれぞれ電子電荷および質量，cは光速度，θはブラッグ角。Gをラウエ関数あるいは干渉関数という。L, M, Nが無限大に近づくとGは各逆格子点に置かれたデルタ関数となる。

執筆者：丸茂 文幸

出典　平凡社「最新 地学事典」