不連続関数（読み）ふれんぞくかんすう（その他表記）discontinuous function

ブリタニカ国際大百科事典 小項目事典

不連続関数
ふれんぞくかんすう
discontinuous function

実数のある区間で定義された実数値関数 f(x) は，その区間内の1点 a において，x→a のとき f(x)＝f(a) を満たすとき，x＝a で連続であるといわれる。もしある区間のすべての点で f(x) が連続ならば f(x) はこの区間で連続であるという。もし関数 f(x) が，ある区間の少なくとも1点で上の条件を満たさないならば，すなわち不連続であるならば，この関数は考えられている区間で不連続関数であるという。通常は，ギャップのある場合，すなわち
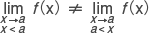の場合を連想しやすいが，振動して x→a が考えられないような場合，連続関数と異なった，不連続関数に固有の性格を表わして，たとえば積分を考えたりしにくくなる。

出典　ブリタニカ国際大百科事典 小項目事典