連続関数（読み）レンゾクカンスウ（英語表記）continuous function

デジタル大辞泉

れんぞく‐かんすう〔‐クワンスウ〕【連続関数】

定義域のすべての点で連続している関数。

出典　小学館

精選版 日本国語大辞典

れんぞく‐かんすう‥クヮンスウ【連続関数】

1. 〘 名詞 〙 数学で、定義域内のすべての点で連続な関数。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

連続関数 (れんぞくかんすう)
continuous function

現代の数学では，関数を写像の意味に用いるので，その場合は連続関数は連続写像と同義語になるが，本項目では実数の集合のうえで定義された実数値関数について述べる。

　実数の集合Eで定義された実数値関数y＝f（x）があるとする。Eとしては，区間またはいくつかの区間の合併などを考える。aをEに属する点（実数）として，点xがEの中から点aに近づくならば，関数f（x）の値がf（a）に近づくとき，すなわち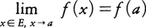，が成り立つとき，関数fは点aにおいて（またはx＝aにおいて）連続であるという。定義域Eの各点で連続な関数を，E上の連続関数という。f，gがE上の連続関数ならばその和，差f±gおよび積f・gはE上の連続関数であり，また，g（x）＝0となる点xを定義域から除いて考えれば，商f/gも連続関数である。関数fの定義域Eの点aでfが連続であるときaをfの連続点と呼び，それ以外のEの点をfの不連続点と呼ぶ。fの定義域に属さない点（すなわち関数が定義されていない点）では，連続，不連続は考えられない。例えばf（x）＝1/xは（－∞，0）∪（0，∞）で定義されているが，x＝0では定義されていないから，0は連続点とも不連続点ともいわない。連続関数fの値域が連続関数gの定義域に含まれているとき，合成関数g◦f，すなわち関数z＝g（f（x））も連続である。

　関数fの定義域が閉区間［a，b］である場合には，fがこの区間で連続ということは，y＝f（x）のグラフがx-y平面上の点（a，f（a））から点（b，f（b））に至る一つの連続曲線（直観的な意味の）となることである。このように考えると，連続関数のいろいろの性質が直観的にとらえやすい。例えば，fが閉区間［a，b］で連続でf（a）≠f（b）ならば，f（a）とf（b）との間の任意の値αに対して，f（c）＝αとなるcがaとbの間にある（中間値の定理）。また，閉区間［a，b］で連続な関数は，その区間で最大値をとる点および最小値をとる点がある。

　関数の定義域がn次元ユークリッド空間（あるいはもっと一般に距離空間，位相空間）の場合も，連続の概念についてはまったく同様に述べることができる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」