保型関数（読み）ほけいかんすう（その他表記）automorphic function

改訂新版　世界大百科事典

保型関数 (ほけいかんすう)
automorphic function

平面領域Dを不変にする一次分数変換を元とする群Gがあり，Dを定義域とする有理型関数fで，Gに属する変換を独立変数にほどこしても値の変わらないもの，すなわち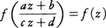，が成り立つようなものを保型関数という。三角関数のような周期関数，楕円関数のような二重周期関数の一般化である。保型関数の概念はH.J.ポアンカレが導入し，代数関数論や微分方程式論に応用して大きな成果をあげた。

　fが非定数であるためには，Gはつぎの性質をもっていなければならない。すなわち，任意の点z∈Dに対して，集合｛r（z）｜r∈G｝はDに集積点をもたない。この性質のあるG（一次分数変換を元とする）をクライン群Klein groupといい，とくにDが円板または半平面のときフックス群Fuchs groupという。fはリーマン面D/Gの上の有理型関数であり，また逆も正しい。

　保型関数には整数論的に重要な側面があり，この立場からの研究も重要である。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」